層流とは
流線流とも呼ばれる層流は、流体内の粒子が滑らかで平行な層を成して移動する流れです。隣接する層間では、最小限の混合しか起こらず、発生する変動は無秩序ではありません。層流は、流体の粘性力が内部の運動力に対して優勢である場合に見られます。これは、乱流とは異なり、流体粒子が不規則かつ無秩序に動くことはなく、渦流や渦が発生することもありません。層流は、比較的低い流速で流れる粘性流体の中で最も一般的なものです。
エンジニアが層流を重視する理由は、流体の混合がほとんどなく、流体の動きが比較的安定していることによって、流体が周囲の固体物体に加える荷重、流体内の混合、および伝熱に影響が及ぶからです。場合によっては、流れの状態を層流に保つために取り組むことがあります。たとえば、手術室では、層流の気流を利用することで、汚染物質を患者から遠ざけます。また、設計によっては、ゴルフボールのように乱流を意図的に作り出すことが有益な場合があります。これは、層流が抗力を増加させるからです。
層流の計算方法と特性の評価方法
層流は滑らかで層状になっているため、エンジニアは方程式を用いて、乱流に起因する流速、速度変動、圧力変動を計算し、特性を評価します。この特性評価では、まず「レイノルズ数」と呼ばれる無次元量を得てから、他の方程式を用いて、層流を設計または測定する際に役立つ他の挙動を捕捉します。
層流の予測：レイノルズ数
1883年、英国の研究者であるOsborne Reynolds氏は単純な管内の水流における層流から乱流への遷移に関する論文を発表しました。この論文には、内部力と粘性力の比から乱流が生じる確率を予測できることが示されています。この無次元の値は「レイノルズ数」と呼ばれています。
レイノルズ数は、次式から求めることができます。
ρ = 流体の密度（kg/m3）
u = 流速（m/s）
L = 代表長さ（パイプ直径、水力直径、相当直径、翼弦長など）（m）
μ = 流体の粘度（Pa·s）
v = 動粘度（m2/s）
Reynolds氏の研究が示すように、レイノルズ数が小さい管内の流れは、流体運動の不安定性を平均流れ方向に垂直な流れに変換するために必要な運動エネルギーを慣性力の形で持たないため、層流として維持されます。流体の粘度に対して流速または密度が増加すると、乱流が生じる確率が高くなります。
層流の重要な特性
層流を扱うエンジニア、物理学者、化学者が考慮すべき特性には、以下のものもあります。
境界層
境界層とは、固体表面に接する流れの層です。流れのタイプが層流の場合、その流れは境界層内で固体表面に平行のまま維持されます。固体表面における流体の速度はゼロであり、これは非すべり境界条件と呼ばれ、速度は固体表面から離れるにつれて単調に上昇し、最終的にバルク流体速度に達します。境界層は層流である場合もあれば、乱流である場合もあります。境界層の厚さと速度プロファイルは、固体表面の抗力と伝熱を左右する重要な特性です。
平板が移動する体積内の層流の数値流体力学（CFD）シミュレーションの例。平板の表面でゼロの相対速度は、バルク速度に達するまで単調に増加する。
拡散
横方向の流れや渦が流体層間の混合を支配する乱流とは異なり、層流の滑らかな流れパターンでは、他の流体層から分離されている各流体層の中に保持されている粒子が、隣接する層間で拡散することで、混合が発生します。拡散とは、高濃度の場所から低濃度の場所へ物質が広がることです。したがって、層流では、特定の物質の濃度が高い層から、隣接する低濃度の層へ粒子が移動します。
表面粗さ
表面粗さは、エンジニアが層流を維持するか乱流にするかを考慮して設計する際に制御できるパラメータです。表面が粗いほど、境界層内の摩擦抗力が大きくなり、せん断応力が粘性力を克服するのに十分な大きさに達すると、流れは層流から乱流へと遷移します。その格好の例がタービンエンジンの圧縮機ブレードの設計であり、この設計では、金属表面の粗さが乱流境界層の発達に大きな影響を与え、それがブレードの性能に影響を及ぼす可能性があります。
速度プロファイル
層流は混沌としていないため、流れの方向に沿って速度がどのように変化するかを明確に把握することができます。これは速度プロファイルと呼ばれます。速度プロファイルは、高速度と低速度が存在する場所を把握し、形状や入口に変更を加えたときに速度にどのような影響が及ぶのかを確認するための簡単な方法です。
層流のモデリング方法
層流では、流体が平行な層を成して流れるため、層流状態における流体の挙動は、流体力学の支配方程式であるナビエ-ストークス方程式を使用して計算することができます。ナビエ-ストークス方程式は、質量、運動量、エネルギーの保存則に基づいて、流体の圧力と速度を記述するものです。円筒形管内または2枚の平板間の単純な流れの特性は、閉形式の解を使用して評価することができますが、より複雑な形状の内部や周囲の流れでは、CFDを用いて流れの体積を離散化し、時間とともに変化する圧力、速度、温度を解析します。
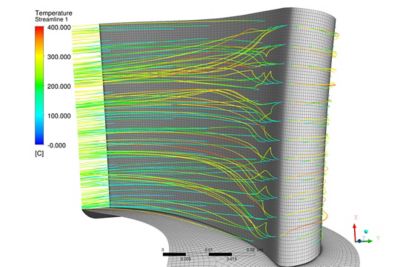
タービンエンジンブレード周りの層流を示すCFDモデル
層流は境界表面の形状に沿って流れるため、層流のモデリングを成功させるための鍵の1つは、その表面に平行なメッシュを生成し（離散化ステップ）、境界層を適切に表現することになります。エンジニアは、多くの場合、タービンブレード用メッシュ生成ソフトウェアである、Ansys TurboGrid™などのツールを使用することで、既知のトポロジーに適した効率的かつ正確な境界層メッシュを自動的に生成します。
CFDプログラムでは、モデル内の各セルの流れを解析するため、均一な形状の歪みやセルサイズの急激な変化によって、解に数値誤差が生じる可能性があります。CFDモデルを作成するエンジニアは、メッシュが適切で効率的であることを確認しながら、時間をかけてメッシュを生成します。これは、セル数によって実行時間が決まるためです。解析を正確かつ効率的に行うためには、効率的なメッシュトポロジーの作成を支援するメッシュ生成機能を備えた流体シミュレーションソフトウェアである、Ansys Fluent®などのツールを使用することが重要です。
層流のモデリングでは、流れがいつ乱流に変わるかを特定するために多くの作業が必要であり、この乱流のモデリングには、標準的なナビエ-ストークス方程式の解析に加えて、追加の数値解析モデルも必要になります。そのため、モデル化している形状で流れを層流に保つことを目指していても、乱流のモデリングを取り入れなければならない場合があります。
過去10年間に層流モデリングの分野で起きた変化の1つは、CFDモデルを解析するためにGPU（グラフィックスプロセッシングユニット）を使用するようになったことです。こうした計算アクセラレータを1つまたは複数使用することで、特定のモデルの実行時間を大幅に短縮できるため、比較的安価なワークステーションでCFD解析を実施したり、同じ時間内でより多くの設計反復を行ったりすることが可能になります。
層流を理解することの重要性
扱う流体の種類を問わず、たとえば管内の流れから航空機の空力特性に至るまで、層流を正しく理解し予測することは、原子力発電所から最新の高性能航空機に至るまで、製品設計において非常に重要な要素となります。前述のように、自分が取り組んでいるプロジェクトの層流を理解することにより、流れ場が層流から乱流に遷移するレイノルズ数の範囲を把握できることもあります。
簡単な例としては、実験室の層流フードがあります。これは、科学者や技術者が危険な物質を扱う際に使用する設備で、空気がフード内に一直線に流れ込み、排出口から排出されることで、安全性が確保される仕組みになっています。また、ゴルフボールのように、抗力を減らすためにできるだけ早く乱流を発生させることが求められます。
ゴルフボールのディンプルを利用して乱流を発生させ、これによって気流をボールの後方に保持することで、後流を小さくし、ボール上の抗力を低減する方法を示す図
層流は、複数の物質を混合させずに流体内で輸送する場合にも重要な役割を果たします。こうしたケースでは、特定の場所に物質を堆積させることを目的として行われることが多くあります。また、半導体製造の分野では、化学蒸着チャンバー設計時に、使用している化学物質を均一に堆積させるために、チャンバー内およびウェハ上に均一な層流を作り出す取り組みが進められています。