Quick Specs
LS-DYNA delivers a diverse array of analyses with extremely fast and efficient parallelization.
Ansys LS-DYNA is the industry-leading explicit simulation software used for applications like drop tests, impact and penetration, smashes and crashes, occupant safety, and more.
Ansys LS-DYNA is the most used explicit simulation program in the world and is capable of simulating the response of materials to short periods of severe loading. Its many elements, contact formulations, material models and other controls can be used to simulate complex models with control over all the details of the problem. Ansys LS-DYNA applications include:
LS-DYNA delivers a diverse array of analyses with extremely fast and efficient parallelization.
January 2025
With the 2025 R1 of Ansys LS-DYNA, we release a new CFD solver and significant enhancements in essential application fields.
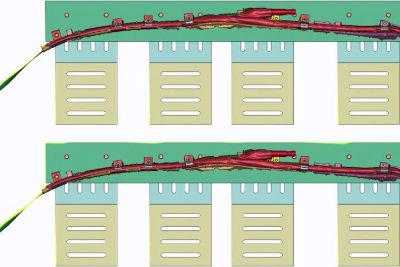
Our novel particle method solver accurately solves the Navier-Stokes equations, offering a tailored approach to simulate gas dynamics in airbag deployment. The solver ensures precise modeling of gas flows, particularly around fabric internal structures, vents, and across different chambers.

We have enhanced the ISPG (Incompressible Smoothed Particle Galerkin) method to model adhesives effectively. This versatile solver now supports various adhesive-related manufacturing processes, including glue dispensing, droplet dispersion, edge and gap filling, glue spreading, thinning, and bonding simulations.
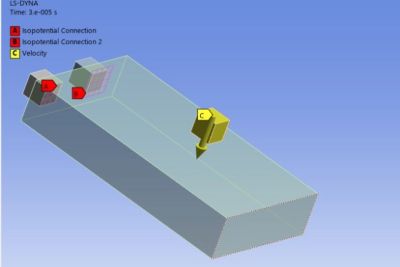
We have introduced new boundary conditions, isopotentials, and short definitions to enable single-cell-level simulations. By exposing ECM/HPPC data and visualizing circuit types, we have implemented significant enhancements to improve simulation accuracy and usability.
Using simulation, doctors can determine the magnitude and location of brain strains, enabling them to improve concussion treatment.

Clinicians are unclear about how to measure the damage incurred by head impacts. Concussions diagnosed by magnetic resonance images (MRIs), computed tomography (CT) scans and blood tests often deliver inconclusive results.
Dr. Michael Power leads clinical care at Beaumont Hospital in Dublin, Ireland, which specializes in the treatment of head injuries — many of which occur during contact sports. Several years ago, he aligned with CADFEM Ireland — Ansys’ channel partner in Ireland — on a mission that would combine engineering simulation with clinical expertise to research the mechanisms of concussion. They sought to understand whether simulation software could help define the causes of concussions, reduce their number and improve concussion treatment.
LS-DYNA CAPABILITIES
Engineers can tackle simulations involving material failure and look at how the failure progresses through a part or through a system. Models with large amounts of parts or surfaces interacting with each other are also easily handled, and the interactions and load passing between complex behaviors are modeled accurately. Using computers with higher numbers of CPU cores can drastically reduce solution times.

LS-DYNA elements, contact formulations, material models and other controls can be used to simulate complex models with control over all the details of the problem.
LS-DYNA RESOURCES

Join us in person on November 15-16 in Novi, Michigan, for an exciting 2-day forum as we showcase keynotes, dozens of user presentations, and networking opportunities with hundreds of expert LS-DYNA users to help accelerate cutting-edge innovation with the user community.

The European LS-DYNA Conference will be held in Baden-Baden, Germany on October 18 and 19 2023. With about 200 technical presentations, top-class keynotes, an accompanying exhibition and numerous international participants from industry and academia, the conference is the central event around LS-DYNA in Europe.
Join us for this webinar to understand battery behavior under normal operating conditions and abuse conditions to optimize battery designs with Ansys LS-DYNA.
In November 2019, Ansys acquired LSTC, the authors of the explicit finite element code LS-DYNA. Ansys LS-DYNA is the most used explicit simulation program, capable of simulating the response of materials to short periods of severe loading.
This webinar presents the use of Ansys LS-DYNA for predicting the vibration caused by trains based on wheel and rail roughness modeling.
Discover how using Ansys LS-DYNA and Ansys optiSLang in tandem meets rising automation demands by joining powerful solvers and providing an opportunity to map and share data between them for advanced optimization and sensitivity investigation.
Learn about the unique capabilities and features of LS-DYNA to efficiently model impact and drop tests.
In this webinar, the BatMac model will be presented along with the test setup and model development. Additionally, capabilities, limitations and future improvement of the battery safety modeling are discussed.
If you're facing engineering challenges, our team is here to assist. With a wealth of experience and a commitment to innovation, we invite you to reach out to us. Let's collaborate to turn your engineering obstacles into opportunities for growth and success. Contact us today to start the conversation.