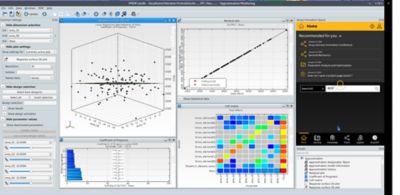
Simulation plays a big role in understanding products and processes, especially complex ones. Parameter-based variation analysis gives you insight into how your design behaves under variability. Multidisciplinary optimization tasks often require a huge number of variables, and it can be difficult to know where to focus. optiSLang’s algorithms and correlation analysis automatically identify the most salient variables, reducing the number of design variables you must worry about. The program’s sensitivity analysis also creates the basis to appropriately formulate the optimization task with respect to choice and number of objectives or possible constraints, helping you quickly zero in on the best approximation model.
Reduced Order Modeling — Ansys optiSLang builds metamodels for rapid feedback and robust design analysis in a fraction of the time it would take to run a simulation to predict a certain design.
Design optimization and parameter identification — Ansys optiSLang’s powerful algorithms and automated workflows build on earlier steps of sensitivity analysis to provide a wizard-driven decision tree to recommend the optimizer with default settings.
optiSLang AI+ — Empowers simulation users with advanced machine learning methods for sensitivity analysis, optimization, and robust design. A more efficient approach offering higher quality prediction of CAE results gives engineers a better understanding of the causal relationship between design parameters and product performance. Design better products in less time.