-
-
Access Free Student Software
Ansys empowers the next generation of engineers
Students get free access to world-class simulation software.
-
Connect with Ansys Now!
Design your future
Connect with Ansys to explore how simulation can power your next breakthrough.
Countries & Regions
Free Trials
Products & Services
Learn
About
Back
Products & Services
Back
Learn
Ansys empowers the next generation of engineers
Students get free access to world-class simulation software.
Back
About
Design your future
Connect with Ansys to explore how simulation can power your next breakthrough.
Free Trials
ANSYS BLOG
November 14, 2022
Hybrid Analytics: A Tool Set for Building Hybrid Digital Twins
A hybrid digital twin is a digital twin that combines both physics and data. In other words, hybrid digital twins do not rely on simulation or machine learning (ML) alone, but take advantage of both methods to leverage all available knowledge about a system. Engineering informs a physics model, while data provides new insights to inform that model. The techniques and tools available to combine physics and data constitute a tool set called hybrid analytics.
By using Ansys Twin Builder and the hybrid analytics tool set you can increase your digital twin accuracy up to 98% or greater.
Hybrid analytics is a set of ML tools for combining physics and data together in different ways. By making smarter choices in selecting your training data and ML techniques, you can open up new possibilities for your hybrid digital twin. One area where this is most evident is in fusion modeling, i.e., the combining of at least two different types of data to train an ML model.
Fusion Modeling: Fusing Physics and Data
To build an ML model, a user supplies input/output (I/O) data and an ML algorithm creates a relationship between the I/O data that can be reused to predict new outputs from different inputs. Naturally, both the choice of training data and the choice of algorithm affect the quality of the outcome. For example, reduced-order models (ROMs) are typically built using simulated data and often use techniques that rely on the physics equations or structure underlying the simulation models. Other statistical techniques are better for sensor data where noise is present. In fusion modeling, at least two different sources of data are used to train a model. This may mean combining different types of simulated data or combining simulation data and sensor data. In any case, combining multiple data sources allows for creating richer ML models for more applications.

Fusion: Residual Modeling
Using both simulated and sensor data is desirable when we want to preserve information known about the system through physics modeling and learn from any available data. Physics-based simulation models make excellent digital twins when the underlying physics of a component or system is well understood and can be modeled with known equations. However, in practice, complete physics models can be difficult to achieve for a variety of reasons, including:
- Friction or losses not fully understood.
- Geometry not fully captured.
- Unmodeled environmental effects.
- Degradation over time.
For example, this could include uncertainty of a motor constant, the inertia of various components, or the amount of friction on the inside wall of a tube. In these situations, the first approach for a solution is to try to learn the parameters of a physics model from available data. ML techniques enable you to learn more accurate parameter values from data and provide estimates for those parameters.
A key benefit of this approach is that the knowledge of the physics behavior is fully preserved in the model. The information that is learned from the data is contained in the values of model parameters. Therefore, even if a model is not fully representing the physics and tries its best to compensate by adjusting parameters, the learned behavior is explainable at least in the context of that model and in relation to other parameter values. Consequently, designers and engineers gain better insights into the root causes of issues and behavior of the system.
Even the best conceived physics models can sometimes fail to fully capture the actual behavior of a system. Specifically, when there are unmodeled physics present in the system, learning better parameter values is still not enough to reach the level of accuracy needed for an application. This is where a fusion model can help by providing highly accurate predictions.
When a gap still remains between the predictions of a calibrated twin and expected behavior, you can build a fusion model to simulate the difference between the predictions of the twin and the data representing the target behavior. This type of fusion modeling is often referred to as residual modeling. In a fusion residual model, the two different data sources are the physics model predictions and the experimental data. For this reason, residual modeling is most used to achieve more accurate predictions in what-if scenarios.

This diagram demonstrates the process of fusion residual modeling, i.e., using physics model predictions and experimental data as the two main sources of data.
A top benefit of this approach is that whatever physics is known for a system is still preserved, but data can help you model whatever is left over due to unknown or misunderstood effects in the system, i.e., the residual data. It is important to note that the fusion portion of the model in general will not explain what is missing, but in combination with the twin outputs it does offer more accurate predictions. In that way, the uncertainty is restricted to the portion of the behavior that was already unknown and nothing is lost by adding the ML piece.
By applying fusion models in this way, ML is enabled in a context that preserves already known physics. Essentially, a fusion residual model can be built to compensate for a very poor physics model. In these cases, the fusion model is more of a data model, and like other data models, the underlying physics can be obscured or lost. Still, even in this instance, a subpar physics model can provide at least some constraints on the ML piece.
Fusion for residual modeling really shines when it is used to improve models that already provide good fidelity but are lacking by 10% or so. In this case, the fusion model may not fully explain the physics of the small residual, but the main physical effects of the system are fully preserved in the physical twin and can be easily accessed.
Fusion: Multifidelity Regression
Another application for fusion modeling is multifidelity regression. In this case, one source of data is taken as the ground truth, and a second source of data approximates that ground truth. Fusion is used when the ground truth data is scarce and the approximate data is abundant. One example of this is in bench testing. Collecting test data can be costly and time consuming. There is a drive to push as much of this testing to the virtual realm as possible to cut costs. Simulation models can be used to replace bench testing, but only if they accurately reproduce the actual behavior of the system. At least a few data points are needed from the bench testing to check the behavior of simulation models. If the simulation model does not provide a high enough fidelity match to the testing data, a fusion model can be built to model the difference between the test data and the model.
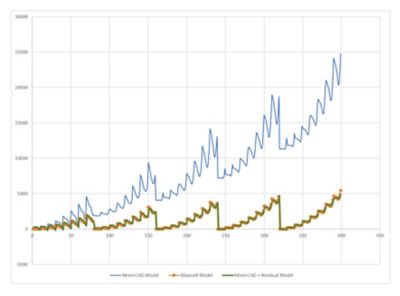
This graph shows an Ansys Maxwell model that generates much higher results than an Ansys Motor-CAD model. However, the Motor-CAD model combined with a fusion residual model performs about the same as the full Maxwell model.
The model with the fusion correction can then be used to accurately simulate other design points or scenarios in which no testing was performed.
The same idea can be used with two sources of simulated data.
For example, a finite element (FEA) model of an electric motor includes full geometry and physical effects to provide very accurate predictions. The tradeoff is that FEA models can take a long time to run. This can make repeated testing on many scenarios difficult. Motors can also be modeled to good approximation faster using 1D or 2D assumptions.
A fusion model uses both types of motor simulation to achieve the best predictions faster. The FEA simulation data is used as an anchor to the correct behavior for a few design points. A 1D model simulates all design points. The fusion model demonstrates the difference between the two simulation models at the design points. The 1D model, plus the fusion correction, is then an accurate prediction for the other design points. The amount of design points needed in the FEA model depends on the correlation between the results of the two models. For example, with higher correlations, you can use FEA design points and rely more on the 1D model.
Explore Hybrid Analytics Firsthand
Digital twins often exist on the edge or in the cloud, in environments where knowledge might be scarce. Hybrid digital twins help overcome this challenge by making use of all data available and providing the best solution for predictive maintenance and performance optimization. While analytics typically refers to learning from data, hybrid analytics is a set of techniques for learning from both experimental data and physics-based simulations. Built from multiple sources of data and physics, fusion models are an important building block for hybrid digital twins that allow for higher accuracy, especially in areas that physics is uncertain.
To learn more about Ansys’ digital twin workflow and hybrid analytics tool set, watch the webinar: How to Get the Most Accurate Twins with Hybrid Digital Twins.