ANSYS BLOG
November 14, 2022
混合分析:用于构建混合数字孪生的工具集
混合数字孪生是将物理和数据结合在一起的数字孪生体。换句话说,混合数字孪生不单独依靠仿真或者机器学习(ML),而是同时发挥两种方法的优势,充分利用有关系统的所有可用知识。工程为创建物理模型提供信息,而数据则向该模型提供新洞察。将物理与数据相结合的方法和工具,构成了被称为“混合分析”的工具集。
通过使用Ansys Twin Builder和混合分析工具集,您可以将数字孪生准确度提高到98%或更高水平。
混合分析是一套以不同方式将物理与数据相结合的机器学习工具。通过更明智地选择训练数据和机器学习方法,您可以为混合数字孪生开辟新的可能性。一个备受瞩目的领域是融合建模,即综合运用至少两种不同类型的数据来训练机器学习模型。
融合建模:融合物理与数据
为了构建机器学习模型,用户需要提供输入/输出(I/O)数据以及在I/O数据之间建立关系的机器学习算法。重复使用该算法,可以预测不同输入产生的新输出。当然,训练数据的选择和算法的选择都会影响结果质量。例如,降阶模型(ROM)通常使用仿真数据来构建,并且通常使用依赖物理方程或仿真模型底层结构的方法。其他统计方法更适用于存在噪声的传感器数据。在融合建模中,至少要使用两种不同的数据源来训练模型。这可能需要结合不同类型的仿真数据或结合仿真数据与传感器数据。在任何情况下,结合多个数据源有利于为更多应用创建更丰富的机器学习模型。

融合:残差建模
如果我们希望通过物理建模保存已知的系统相关信息,并从任何可用数据中学习,可以同时使用仿真数据和传感器数据。只要充分理解组件或系统的基本物理特性并且能用已知方程建模,就可以基于物理的仿真模型创建高质量数字孪生体。然而在实际情况中,由于各种原因,难以实现完整的物理模型,包括:
- 不能充分理解摩擦或损耗
- 不能完全捕获几何结构
- 不能为环境影响建模
- 随时间发生退化
例如,这可能包括电机常数的不确定性、各种组件的惯性或管道内壁上的摩擦量。在这些情况下,首选解决方法是尝试从可用数据中学习物理模型的参数。机器学习方法能够帮助您从数据中学习到更准确的参数值,并为这些参数提供估计值。
这种方法的主要优势在于,模型中完全保留了物理行为知识。从数据学习到的信息包含在模型参数的值中。因此,即使模型不能完全表达物理特性,也可通过调整参数尽量予以补偿,习得的行为至少在该模型的情景下具有可解释性,并且与其他参数值存在关联。因此,设计人员和工程师可以深入地了解问题根源和系统行为。
即便构思最佳的物理模型有时也无法完全捕获系统的实际行为。具体而言,当系统中存在未建模的物理时,学习更好的参数值仍不足以实现应用所需的精度水平。此时融合模型通过提供高度准确的预测,能够起到帮助作用。
当经过校准的孪生预测与预期行为之间仍存在差异时,您可以构建融合模型来仿真孪生的预测和表达目标行为的数据之间的差异。这种类型的融合建模通常被称为残差建模。在融合残差模型中有两种不同的数据源,分别是物理模型预测和实验数据。因此,残差建模最常用于在假设场景下实现更准确的预测。

该图展示了融合残差建模的过程,即:使用物理模型预测和实验数据作为两个主要数据源。
这种方法的最大优势在于,无论系统中存在哪些仍被保留的已知物理信息,数据都能帮助您建模因系统中存在未知或误解而出现的剩余部分,即残留数据。值得注意的是,模型的融合部分一般不会解释缺失的内容,但与孪生输出结合,确实能提高预测准确度。通过这种方法,不确定性被限制在未知的行为部分,而添加机器学习部分不会损失任何东西。
以这种方法应用融合模型,能够在保留已知物理信息的情况下运行机器学习。本质上,可以构建融合残差模型来补偿质量极差的物理模型。在这些情况下,融合模型更像是数据模型,并且与其他数据模型一样,基本物理特性可能会被掩盖或丢失。然而,即便在这种状况下,低质量物理模型至少依然能对机器学习部分产生一定的约束。
当融合残差建模被用于改进已经提供高保真度结果但仍存在大约10%差异的模型时,可产生极佳的效果。在这种情况下,融合模型可能无法完全解释少量残留的物理效应,但系统的主要物理效应完全保留在物理孪生中,并且可以轻松访问。
融合:多保真度回归
融合建模的另一个应用是多保真度回归。在这种情况下,一个数据源被视为地面实况,另一个数据源与这个地面实况近似。当地面实况数据稀缺而近似数据丰富时,可以使用融合功能。这方面的一个例子是工作台测试。收集测试数据成本高昂且非常耗时。为了节省成本,需要尽可能多地在虚拟环境下开展测试。仿真模型可用于替代工作台测试,但它们必须能准确再现系统的实际行为。我们至少需要一些来自工作台测试的数据点,以检查仿真模型的行为。如果仿真模型不能提供与测试数据足够高的保真度匹配,可以构建融合模型,为测试数据与仿真模型之间的差异建模。
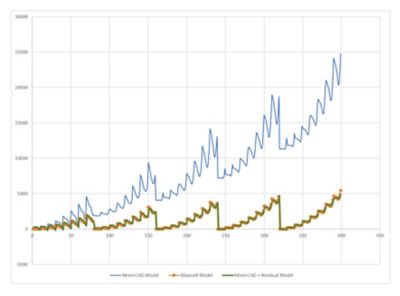
该图显示了Ansys Maxwell模型生成的结果准确度远高于Ansys Motor-CAD模型。然而,如果Motor-CAD模型与融合残差模型结合,性能可媲美完整的Maxwell模型。
随后可将具有融合校正功能的模型,用于准确仿真未开展测试的其他设计点或场景。
该方法同样适用于两个仿真数据源。
例如,电机的有限元(FEA)模型包含完整的几何结构和物理效应,能提供极为准确的预测。但代价是有限元模型可能需要较长时间来运行。这就很难在众多场景上开展重复测试。使用1D或2D假设条件,也可以更快地对电机进行建模以获得良好的近似度。
融合模型同时使用两种类型的电机仿真,以更快实现最佳预测。对于一些设计点,有限元仿真数据可用作正确行为的锚点。1D模型可仿真所有设计点。融合模型体现了两个仿真模型在这些设计点上的差异。随后将1D模型与融合校正相结合,为其他设计点提供准确预测。有限元模型中所需的设计点数量取决于两个模型结果之间的相关性。例如,如果具有较高的相关性,您可以使用有限元设计点并主要依靠1D模型。
亲自探索混合分析
数字孪生通常存在于边缘或云端,而这两种环境下的相关知识可能较稀缺。混合数字孪生利用所有可用数据,并为预测性维护和性能优化提供最佳解决方案,帮助克服这一挑战。分析通常是指从数据中学习,而混合分析是一套从实验数据和基于物理的仿真中学习的方法。基于多个数据源和多种物理,融合模型是混合数字孪生的重要组成部分,有利于提高仿真精度,尤其是在物理信息不确定的领域。
如欲了解有关Ansys数字孪生工作流程和混合分析工具集的更多信息,请观看网络研讨会:如何使用混合数字孪生获得最准确的孪生。