ANSYS BLOG
October 5, 2022
Finding Resolution: How to Use the Point Spread Function in OpticStudio to Assess Diffraction-Limited Imaging Systems
Diffractive optics is an important field in optical engineering that takes advantage of the full properties of natural light to develop optical systems and their related components — including lenses and mirrors found in microscopes, telescopes, or cameras. Essentially, diffractive optics is a branch of physics related to image creation in response to varying wavelengths of light on an object. For example, using mirrors that focus light to create an image are central to high-speed photography. Today, diffractive optical elements are used in many industries, such as aerospace, communications, and medicine.
Due to the physics of diffraction, the principle resolution — or the degree of detail visible as it applies to an optical system — is limited. This can be caused by a host of factors, from lens imperfections to misalignment. When an optical system’s resolution performance hits its theoretical limit, it is said to be diffraction limited. Therefore, it’s important to characterize the resolution of a diffraction-limited imaging system, such as a microscope, to understand its performance.
Imaging system performance relates to a system’s resolution, which can vary by definition. Fourier Ring Correlation is used in super-resolution microscopy to evaluate resolution — for diffraction-limited microscopes, Rayleigh or Sparrow criterion is used. Microbeads can be used to measure both, acting as point emitters to form a point spread function (PSF), which can estimate the resolution in an image with size being a variable. However, if you’re looking for a more objective evaluation, the PSF in Ansys OpticStudio can help.
In this blog post, we’ll discuss how the PSF can be calculated in OpticStudio to measure the resolution of a diffraction-limited imaging systems more objectively, using microscopes as a relevant example.
Multi-Configuration Editor for Coherent Imaging in Microscope Design
The point of reference for this method is a TL4X-SAP objective lens (4, 0.2 NA), and a TTL200 tube lens, available as black boxes from THORLABS. The Rayleigh criterion works on several basic assumptions, including a perfectly clear, unaberrated aperture stop and incoherent illumination. It’s a subjective metric used to discern two PSFs, as influenced by the observer, and the type of information needed from the microscopic images.
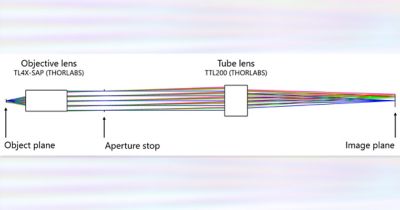
Microscope design composed of black box elements from THORLABS. The magnification is 4X, and the numerical aperture (NA) is 0.2.
Step 1: Establish the field set-up for the multi-configuration method in OpticStudio to analyze the microscope resolution. Remove all information but the on-axis field and convert it to Object Height.
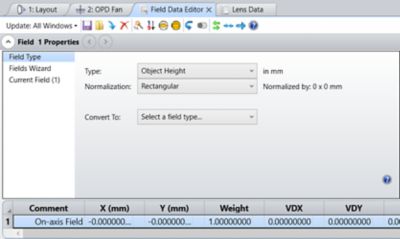
Field setup for the multi-configuration method to analyze the microscope resolution. Only the on-axis field is kept, and it has been converted to Object Height.
Step 2: Create two configurations in OpticStudio with a single YFIE operand, specifying a value of 1.8e-3 mm in the second configuration.
Step 3: Use a Huygens PSF and Huygens PSF Cross Section to analyze the overlap of the two PSFs in the image plane. Both analyses can perform a coherent sum of the individual PSFs across two configurations within OpticStudio.
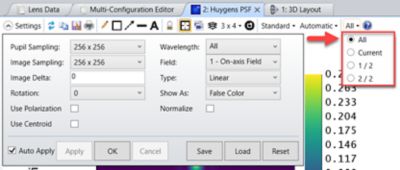
Huygens PSF settings. By checking all configurations from the menu bar, a coherent sum is performed of the individual PSFs.
In the case of indistinguishable results, from the Rayleigh criterion, the separation distance of the fields can be increased in OpticStudio and the results re-evaluated as the PSFs begin to separate in the image plane, resulting in two distinct peaks.
In OpticStudio, you can also define how the peaks should be separated in post-processing to make the criterion more objective. In other words, the greater the field separation, the more distinguishable the PSFs become.
Inadequate physical pixel size further degrades microscope resolution. OpticStudio can also be used to account for the physical pixel size of a hypothetical detector, which is used to measure the illumination of a light source in optical spectrometry applications to get an image as you would see it from the microscope.
To learn more on this topic, read this blog titled How to Determine the Resolution of Diffraction-limited Imaging Systems Using the Point Spread Function in Ansys Zemax OpticStudio.