Les paramètres S, qu'est-ce que c'est ?

Les paramètres de diffusion (également appelés paramètres S) renvoient aux éléments d'une matrice mathématique décrivant le comportement d'un réseau (ou circuit) électrique lorsqu'il est stimulé par un signal électrique.

Sous hautes fréquences (au-delà de quelques gigahertz), il devient difficile de mesurer directement les tensions et les courants. C'est pourquoi on recourt aux paramètres S pour décrire les relations entrée-sortie des ondes de puissance entre les ports d'un réseau électrique.

Les ingénieurs électriciens peuvent appliquer les paramètres S à un large éventail de conceptions d'ingénierie, tels que les systèmes de communication, les circuits intégrés et les circuits imprimés (PCB), les circuits hyperfréquences et les circuits radiofréquences (RF).

En particulier, les paramètres S diffèrent des autres types de paramètres employés, tels que les paramètres Y, Z et ABCD, en ce sens qu'ils utilisent des charges adaptées (au lieu de terminaisons en circuit ouvert ou en court-circuit) pour caractériser les réseaux électriques.

Les expressions mathématiques nous aident à décrire le monde qui nous entoure. Dans les réseaux électriques à petits signaux, les équations linéaires relient des quantités indépendantes de tensions et de courants à des quantités dépendantes (également des tensions et des courants).

Ainsi, même les circuits les plus complexes peuvent être réduits à de simples « boîtes noires », dans lesquelles les tensions et les courants de sortie sont reliés aux tensions et aux courants d'entrée par des relations mathématiques simples.

Avant l'apparition des circuits haute fréquence, les paramètres Y et Z étaient les principales méthodes de caractérisation des performances du réseau. Cependant, à des fréquences plus élevées, il devient difficile d'associer directement les performances du réseau aux tensions et aux courants, notamment dans les réseaux incorporant des lignes de transmission telles que des guides d'ondes.

Par conséquent, les paramètres S référencent les éléments d'une matrice de diffusion, décrivant les caractéristiques de diffusion d'une onde de tension qui se propage à travers un réseau ou un circuit électrique. Ils dérivent du concept d'onde de diffusion popularisé par E.W. Matthews, Kaneyuke Kurokawa et d'autres.

Que sont les ondes progressives ?

Lorsqu'une onde électromagnétique progressive rencontre un obstacle ou traverse un milieu diélectrique différent, on dit qu'elle est « diffractée ». Ainsi, les paramètres S décrivent comment les courants et les tensions qui se propagent le long d'une ligne de transmission sont « diffractés » lorsqu'ils rencontrent une discontinuité formée par un composant ou un réseau. Cette discontinuité provient d'un décalage entre l'impédance du composant ou du réseau et l'impédance caractéristique de la ligne (ou impédance de charge).

Lorsqu'un signal incident arrive à un port réseau, une partie de son énergie est réfléchie à partir du port, tandis que le reste est transmis (ou diffracté) aux autres ports du réseau, ce qui entraîne une amplification ou une atténuation du signal.

Calcul des paramètres S

Étant donné que les paramètres S décrivent les caractéristiques des ondes incidentes et réfléchies à des fréquences spécifiques, les ingénieurs doivent spécifier ces fréquences, ainsi que les impédances caractéristiques du dispositif testé (DUT).

Les paramètres S se révèlent les plus utiles (et sont largement utilisés) dans la conception, l'analyse et l'optimisation des circuits hyperfréquences et radiofréquences (RF) (300 MHz - 300 GHz). Il n'est ainsi plus nécessaire de modéliser les caractéristiques internes d'un appareil RF, permettant aux ingénieurs de se concentrer uniquement sur leurs comportements d'entrée-sortie.

Les ingénieurs calculent les paramètres S en mesurant les tensions et les courants à chaque port de circuit. Ces paramètres sont des coefficients sans dimension calculés comme des rapports de tension des ondes incidentes et transmises (ou réfléchies). La matrice de diffusion pour un réseau multiport (matrice à x ports) comprend x^{2} paramètres S, chaque paramètre représentant un chemin d'entrée-sortie dans le circuit.

Chaque paramètre est un nombre complexe sans dimension, la partie réelle désignant l'amplitude du signal et la partie imaginaire la phase du signal, à la fréquence de test. L'amplitude peut être exprimée sur une échelle linéaire ou logarithmique (dans ce cas, elle est exprimée en décibels). La phase est normalement exprimée en degrés, ou occasionnellement en radians.

Les ingénieurs doivent également spécifier les conditions suivantes lors de la mesure des paramètres S :

• Fréquence du test
• Impédance caractéristique (généralement 50 Ω)
• Attribution de numéros de port
• Autres conditions, telles que le courant de polarisation, la température et la tension de commande

Représentation des paramètres S

Les paramètres S sont affichés sous forme de matrice, où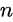 indique le port d'entrée.

Ainsi, la matrice S d'un réseau à deux ports s'écrit comme suit :

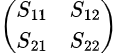
Où :

• S_{11} est le coefficient de réflexion du port d'entrée
• S_{22} est le coefficient de réflexion du port de sortie
• S_{12} est le coefficient de transmission du port d'entrée (ou « gain de tension inverse »)
• S_{21} est le coefficient de transmission (ou « gain de tension directe »)

Notez que les paramètres diagonaux sont appelés « coefficients de réflexion » parce que les entrées et sorties de signal se produisent sur un seul port, tandis que les paramètres hors diagonale sont appelés « coefficients de transmission », indiquant les entrées et les sorties sur différents ports. La règle est similaire pour toute matrice de {n}ème ordre.

Les paramètres S peuvent être tracés sur un diagramme linéaire ou polaire, dans lequel chaque point représente une fréquence de test.

Paramètres S dans la conception de circuits RF

Les ingénieurs mesurent les paramètres S pour déterminer des caractéristiques telles que la perte, le gain, l'impédance et le rapport d'onde stationnaire de tension (VSWR) dans un réseau linéaire haute fréquence (RF ou hyperfréquence). Diverses normes électriques, notamment 10 GbE, SATA, PCIe et Fiber Channel, utilisent toutes des paramètres S pour formuler leurs procédures de test de conformité.

Les principales applications sont les suivantes :

• Conception d'amplificateur : dans la conception d'amplificateurs RF, les ingénieurs utilisent les paramètres S pour analyser le gain, la stabilité et la linéarité afin d'obtenir une bande passante maximale et des résultats d'adaptation d'entrée/sortie.
• Conception de filtre : les paramètres S aident les ingénieurs à évaluer la réponse en fréquence, la perte par insertion, la perte par réflexion et la sélectivité dans les filtres passe-haut, passe-bande, passe-bas et coupe-bande.
• Caractérisation de la réponse en fréquence : du fait que les paramètres S varient avec les fréquences appliquées, ils peuvent révéler les réponses caractéristiques des circuits RF sur une large gamme de fréquences, permettant la caractérisation de la largeur de bande, de la résonance, des influences parasites et d'autres réponses fréquence-dépendantes.
  
• Caractérisation de la réponse de la transmission : les paramètres S révèlent comment les circuits RF transfèrent la puissance entre les ports, caractérisant les réponses en perte, gain et déphasage.
  
• Adaptation d'impédance : en examinant les paramètres S (en particulier les coefficients de réflexion), les ingénieurs peuvent obtenir une adaptation d'impédance optimale entre les composants du circuit et maximiser le transfert de puissance entre les sources et les charges.
  
• Analyse des interconnexions : les paramètres S permettent de caractériser la diaphonie ,l'intégrité du signal, les décalages d'impédance et d'autres effets dans les interconnexions et les lignes de transmission.
  
• Analyse de l'intégrité du signal : la puissance du signal peut être affectée négativement par l'atténuation, les réflexions et les décalages d'impédance, que les ingénieurs peuvent atténuer en examinant les paramètres S dans un réseau.
• Conception de circuit : les ingénieurs utilisent les paramètres S pour évaluer différentes configurations de circuit RF afin d'optimiser les spécifications de conception pour le gain, la perte, le transfert de puissance et l'adaptation d'impédance.
• Analyse réseau : les ingénieurs peuvent analyser les performances de réseaux complexes (comme le déphasage, le gain et la réponse en fréquence) en raccordant en cascade les paramètres S des composants individuels.

Les paramètres S fournissent aux ingénieurs des informations précieuses sur les performances des réseaux électriques linéaires, tels que les circuits RF, les amplificateurs et les filtres. Ces informations sont notamment les suivantes :

• Détails de l'amplitude, de la phase, de la réflexion et de l'atténuation du signal
• Emplacements des pertes de signal et des décalages d'impédance
• Paramètres de ligne de transmission, tels que R, L, C, G, TD et Z0

De plus, les paramètres S sont plus faciles à mesurer que les paramètres Y ou Z aux fréquences RF, car ils ne nécessitent pas de circuits ouverts ou de courts-circuits. Ils sont également facilement convertis en d'autres formats de paramètres, y compris les paramètres ABCD, H, T, Y, et Z, offrant une certaine flexibilité dans l'analyse et la conception de circuits.

Les paramètres S sont également facilement enregistrés sous forme de fichiers Touchstone (fichiers texte ASCII) lisibles par un logiciel de simulation de circuit.

Bien que l'utilisation des paramètres S présente de nombreux avantages, elle comporte également quelques limites :

• Les paramètres S ne peuvent être utilisés que dans l'analyse du domaine fréquentiel (réponse fréquentielle des signaux), à l'exclusion du domaine temporel (réponse transitoire des signaux).
• Ils ne permettent pas de caractériser les réseaux en termes d'ondes de tension et de courant simultanément. Pour cela, les ingénieurs utilisent les paramètres ABCD. En outre, il est plus facile de cascader les paramètres ABCD que les paramètres S.
• La plupart des charges de silicium se comportent de manière non linéaire.

Les circuits numériques sont en grande partie régis par des seuils de tension, dans lesquels les ingénieurs doivent comprendre le flux d'énergie électrique, nécessitant donc une analyse du domaine temporel. L'analyse du domaine temporel est également importante dans les conceptions de circuits avec antennes, dans lesquelles les ingénieurs doivent caractériser les réflexions et les signaux parasites.

L'analyse du domaine fréquentiel simplifie l'analyse mathématique et fournit une compréhension intuitive de la qualité du système. Les ingénieurs utilisent des termes tels que gain, largeur de bande, fréquence de résonance et déphasage lorsqu'ils souhaitent référencer les éléments à dépendance temporelle des caractéristiques de fréquence. 

En outre, il est possible de convertir des informations de signal entre les domaines fréquentiel et temporel en utilisant des opérateurs mathématiques appelés transformées (par exemple, transformées de Fourier), bien que cela puisse introduire des erreurs.

Dans le modèle matriciel, une « boîte noire » représente un réseau électrique contenant des composants d'interconnexion, tels que des transistors, des condensateurs, des résistances et des inductances, qui interagissent avec d'autres circuits par l'intermédiaire de divers ports.

Le réseau peut contenir un nombre indifférent de composants, à condition qu'il se comporte linéairement lorsque de petits signaux incidents lui sont appliqués. Il peut également inclure des composants typiques de systèmes de communication, tels que des atténuateurs, des amplificateurs, des coupleurs et des filtres, à condition qu'ils fonctionnent également de manière linéaire.

Paramètres S « petits signaux »

Dans la grande majorité des cas, les paramètres S s'appliquent aux réseaux monofréquence à petits signaux. Dans ces réseaux, le signal est suffisamment petit pour que la compression de gain ou d'autres effets non linéaires soient négligeables. Ainsi, les paramètres S « petits signaux » sont simplement calculés comme les rapports de tension des ondes réfléchies et incidentes.

Les réseaux linéaires comprennent :

• Les réseaux sans perte qui ne dissipent pas de puissance, de sorte que la somme des puissances incidentes est égale à la somme des puissances réfléchies sur tous les ports. Cela implique que la matrice de paramètres S est unitaire.
• Les réseaux passifs avec perte, dans lesquels la somme des puissances incidentes dépasse la somme des puissances sortantes, ce qui signifie que le réseau dissipe la puissance.
• Les réseaux passifs réciproques, composés uniquement de matériaux réciproques qui influencent le signal transmis. Les câbles, les répartiteurs, les atténuateurs et les combineurs sont autant d'exemples de réseaux réciproques. Dans ce cas, la matrice de paramètres S est égale à sa transposée, de sorte que S_{ij} = S_{ji}
  
  

Paramètres S « grands signaux »

À mesure que la puissance du signal d'entrée augmente, des effets non linéaires tels que la compression de gain deviennent perceptibles. Par conséquent, les paramètres S « grands signaux » varient en fonction des niveaux de puissance d'entrée. Ceux-ci sont également appelés « paramètres S en fonction de la puissance ».

Les ingénieurs basent leurs mesures de paramètres S « grands signaux » sur une simulation de balance harmonique du réseau, qui est une méthode d'analyse du domaine fréquentiel appliquée aux circuits non linéaires. Ils sont également calculés sous forme de rapports de tension des ondes réfléchies et incidentes.

Paramètres S en mode mixte

Les ingénieurs doivent souvent vérifier les calculs des paramètres S par rapport aux courbes gain-fréquence ou aux abaques de Smith. Ils traceront alors la courbe des paramètres S en mode mixte. Les ingénieurs utilisent ces paramètres pour caractériser la paradiaphonie (NEXT) et la télédiaphonie (FEXT) dans les réseaux différentiels.

Paramètres S à deux ports

Les ingénieurs utilisent généralement des paramètres S à deux ports dans l'analyse réseau, qui servent également de modèle pour les matrices de paramètres S d'ordre supérieur dans les réseaux plus grands. La relation entre ondes réfléchies et ondes incidentes dans les réseaux à deux ports est donnée par :

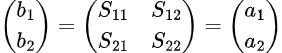
où a_{1} et b_{1} sont respectivement les amplitudes d'onde incidente et réfléchie au port 1, et de même pour a_{2} et b_{2} au port 2.

Les ingénieurs déduisent les propriétés réseau suivantes à partir de mesures de paramètres S à deux ports :

• Perte par insertion
• Perte par réflexion en entrée
• Affaiblissement de réflexion en sortie
• Gain linéaire scalaire
• Gain linéaire complexe
• Gain logarithmique scalaire
• Gain inverse et isolation inverse
• Coefficient de réflexion
• Rapport d'onde stationnaire de tension

Comme indiqué précédemment, les paramètres S aident les ingénieurs à décrire la réponse d'un réseau électrique général à {n} ports, dans lequel les signaux sont appliqués et réfléchis sur n'importe lequel des ports. Ainsi, un paramètre S_{21} décrit une réponse réseau sur le port 2 à partir d'un signal incident sur le port 1. Les paramètres S sont généralement appliqués aux réseaux à un et deux ports.

Les mesures des paramètres S à trois ports s'avèrent plus difficiles, bien que les ingénieurs puissent les modéliser à l'aide d'un logiciel spécialisé. En outre, les fabricants d'appareils peuvent facilement obtenir des mesures de paramètres S multiports, mais les ingénieurs doivent toujours vérifier leur précision.

Utilisation des analyseurs de réseau vectoriels (VNA)

Les ingénieurs en intégrité du signal utilisent régulièrement des analyseurs de réseau vectoriels pour évaluer les performances des circuits RF et hyperfréquences dans diverses conditions de fonctionnement. En conséquence, ils « de-embed », mettent en cascade et visualisent régulièrement une quantité significative de données de paramètres S, en effectuant une combinaison d'analyse théorique et d'expérimentation. Le processus implique typiquement :

• Une analyse théorique du modèle ou schéma de circuit, en appliquant la théorie électromagnétique, la théorie des lignes de transmission et la théorie des circuits pour dériver des équations mathématiques
• Une simulation du comportement du circuit à l'aide d'un logiciel spécialisé (basé sur les équations dérivées) pour extraire les paramètres S
• Une expérimentation d'un analyseur de réseau vectoriel pour extraire les valeurs des paramètres S sur une gamme de fréquences
  
• Le « de-embedding » (soustraction) des contributions des paramètres S des composants individuels d'un circuit si nécessaire
  

Pendant les essais, les ingénieurs transmettent un signal connu d'une source VNA dans un DUT afin de mesurer les altérations du signal lorsqu'il traverse le DUT. Ces altérations sont captées par un récepteur (ou un groupe de récepteurs) connecté au VNA.

Une configuration de VNA type comprend :

• Un oscillateur à balayage (généralement un synthétiseur)
• Une unité d'affichage d'informations
• Deux ports ou plus (souvent connectés à des coupleurs bidirectionnels et à un dispositif de mesure de rapport complexe)
• Des câbles RF

En option, un dispositif de commande de la tension ou du courant de polarisation ou un contrôleur pour stocker des données peut éventuellement être inclus.

Un analyseur de réseau vectoriel capture les réponses en fréquence d'un composant unique (ou d'un groupe de composants, passifs ou actifs) dans un réseau RF. Il mesure la puissance d'un signal donné, capturant sa phase et son amplitude.

Les ingénieurs peuvent déduire diverses caractéristiques du dispositif à partir de ces mesures d'amplitude et de phase, y compris les caractéristiques de retard de groupe, d'impédance, de retour et de perte par insertion.

Les VNA sont des instruments à trajet unique ou multiple comportant plusieurs ports, où des stimuli peuvent être appliqués à l'un des ports, de telle sorte que :

• Un VNA à deux ports et à un chemin renvoie des valeurs de signal réfléchies et transmises au port d'entrée 1 (S_{11} et S_{21}, respectivement). Cependant, le DUT doit être inversé pour obtenir les paramètres opposés au port 2 (S_{22} et S_{12}).
• Un VNA à deux ports et deux voies peut également inverser le flux de signal, ce qui signifie que des mesures peuvent être effectuées dans les deux sens pour extraire les coefficients de réflexion et de transmission à n'importe quel port.

En outre, la position du plan de référence, où les étalonnages sont effectués, influence les mesures VNA.

Erreurs de mesure

Les sources d'erreurs de mesure sont les suivantes :

• Variations des réponses en fréquence, causées par de légères variations des réponses en fréquence des récepteurs du VNA
• Variations des impédances des ports, causées par de légères différences entre l'impédance de référence caractéristique et l'impédance d'entrée au niveau du port de test
• Erreurs de directionnalité, dans lesquelles des parties des ondes incidentes et réfléchies se heurtent les unes aux autres, affectant les mesures dans les deux sens
  
• Erreurs d'isolation, dans lesquelles une petite partie du signal incident sur un port peut fuir dans le canal récepteur d'un autre port, entraînant une diaphonie.
  

Visualisation des paramètres S

La visualisation constitue une première étape importante dans l'analyse des données des paramètres S. Les données de phase et d'amplitude peuvent être tracées en coordonnées cartésiennes ou polaires. Un abaque de Smith est un tracé polaire utilisé dans l'analyse des réseaux d'adaptation.

Pour effectuer des calculs de paramètres S avec précision, il est indispensable de posséder une solide compréhension de la théorie des circuits RF, une expérience avec les logiciels de simulation et un accès à un équipement fiable.

La conception de circuits RF est une tâche complexe, impliquant de multiples itérations. La précision, la complexité du circuit et les outils disponibles déterminent l'approche.

Voici les étapes d'une approche typique de la conception de paramètres S dans un circuit RF haute fréquence :

• Configuration du circuit : dans la conception de la configuration du circuit, l'ingénieur prend en compte la topologie des composants du circuit, des lignes de transmission et des interconnexions, en accordant une attention particulière à l'adaptation d'impédance et à l'intégrité du signal.
• Sélection des composants : l'ingénieur sélectionne les amplificateurs, mélangeurs, filtres et autres composants en fonction des exigences, des caractéristiques d'équilibrage en gain, gestion de puissance, réponse en fréquence, etc.
• Simulation et optimisation : l'ingénieur programme un modèle de circuit, des interconnexions et des propriétés de composant, ainsi que d'autres paramètres dans un outil logiciel spécialisé pour obtenir des valeurs de paramètres S simulées. Il ajuste ensuite avec précision les entrées (telles que la longueur des lignes de transmission) pour atteindre des valeurs optimales de paramètre S en largeur de bande, gain, adaptation d'impédance, etc.
  
• Prototypage : une fois les paramètres souhaités obtenus, l'ingénieur construit un prototype de circuit à l'aide d'un analyseur de réseau vectoriel pour mesurer les valeurs réelles des paramètres S.
• Validation : pour conclure le processus, l'ingénieur peut comparer les valeurs des paramètres S du VNA avec celles simulées. Toute divergence l'invite à affiner la conception du circuit et la sélection des composants, en répétant le processus jusqu'à ce que les matrices S mesurées et simulées soient alignées.
  

Le passage de la transmission de données parallèle à la transmission de données série à grande vitesse donne lieu à une série de nouveaux défis en matière de conception de semi-conducteurs. Avec des débits de données proches du gigabit par seconde, transmettant plus de bits à chaque interconnexion, plusieurs liaisons série fonctionnant en parallèle seront nécessaires, ce qui entraînera des pertes d'interconnexion haute fréquence et une augmentation de la diaphonie.

Il devient donc essentiel de caractériser le couplage électromagnétique dans les puces de semi-conducteurs.

Le logiciel de modélisation électromagnétique (EM) Ansys RaptorH ™ a été conçu pour la configuration optimale des circuits semi-conducteurs, combinant le moteur Ansys HFSS™ et le logiciel Ansys RaptorH dans un seul et même package pratique.

Pris en charge par toutes les principales fonderies de silicium, le traitement distribué haute vitesse du logiciel RaptorH fournit une modélisation précise et éprouvée des paramètres S et RLCk en quelques minutes. Visitez la page dédiée au logiciel Ansys RaptorH pour plus d'informations.

∑_(i=1)^n I_i=0

Ressources connexes