-
-
Access Free Student Software
Ansys empowers the next generation of engineers
Students get free access to world-class simulation software.
-
Connect with Ansys Now!
Design your future
Connect with Ansys to explore how simulation can power your next breakthrough.
Countries & Regions
Free Trials
Products & Services
Learn
About
Back
Products & Services
Back
Learn
Ansys empowers the next generation of engineers
Students get free access to world-class simulation software.
Back
About
Design your future
Connect with Ansys to explore how simulation can power your next breakthrough.
Free Trials
TOPIC DETAILS
What Are S-parameters?
Scattering parameters — also known as S-parameters — refer to the elements in a mathematical matrix describing the behavior of an electrical network (or circuit) when it is being stimulated by an electrical signal.
At high frequencies (exceeding a few gigahertz), it becomes difficult to measure voltages and currents directly. Consequently, S-parameters describe the input-output relationships of power waves between the ports of an electrical network.
Electrical engineers can apply S-parameters to a wide range of engineering designs, including communication systems, integrated circuits and printed circuit boards (PCBs), microwave circuits, and radio frequency (RF) circuits.
Notably, S-parameters differ from other types of parameters in use — such as Y-parameters, Z-parameters, and ABCD parameters — in that they use matched loads (instead of open-circuit or short-circuit terminations) to characterize electrical networks.
Applications of S-parameters
Mathematical expressions help us describe the world around us. In small-signal electrical networks, linear equations relate independent quantities of voltages and currents to dependent quantities (also voltages and currents).
Thus, even the most complex circuits can be reduced to simple “black boxes,” in which output voltages and currents are related to input voltages and currents through simple mathematical relationships.
Before the appearance of high-frequency circuits, Y- and Z-parameters were the primary methods of characterizing network performance. However, at higher frequencies, it becomes difficult to relate network performance directly to voltages and currents, especially in networks incorporating transmission lines such as waveguides.
Hence, S-parameters reference the elements of a scattering matrix, describing the scattering characteristics of a voltage wave propagating through an electrical network or circuit. They derive from the scattering wave concept popularized by E.W. Matthews, Kaneyuke Kurokawa, and others.
What are Traveling Waves?
When a traveling electromagnetic wave meets an obstruction or crosses a dissimilar dielectric medium, it is said to “scatter.” Thus, S-parameters describe how currents and voltages propagating along a transmission line are “scattered” as they meet a discontinuity formed by a component or a network. This discontinuity stems from a mismatch between the component or network’s impedance and the line’s characteristic impedance (or load impedance).
As an incident signal arrives at a network port, some of its energy is reflected back away from the port, while the rest is transmitted (or scattered) to the other ports in the network, resulting in amplification or attenuation of the signal.
Calculating S-parameters
Since S-parameters describe the characteristics of incident and reflected waves at specific frequencies, engineers must specify these frequencies, together with the characteristic impedances of the device under test (DUT).
S-parameters prove most useful (and are widely used) in the design, analysis, and optimization of microwave and radio frequency (RF) circuits (300 MHz - 300 Ghz). They remove the need to model an RF device’s internal characteristics and allow engineers to focus on their input-output behaviors only.
Engineers derive S-parameters by measuring voltages and currents at each circuit port. These parameters are dimensionless coefficients calculated as voltage ratios of incident and transmitted (or reflected) waves. The scattering matrix for a multiport network (n-port matrix) comprises 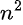 S-parameters, with each parameter representing an input-output path in the circuit.
S-parameters, with each parameter representing an input-output path in the circuit.
Each parameter is a dimensionless complex number, with the real part denoting the signal’s amplitude and the imaginary part denoting the signal’s phase, at the test frequency. The amplitude may be expressed on either a linear or logarithmic scale (in which case it is expressed in decibels). The phase is normally expressed in degrees, or occasionally in radians.
Engineers must also specify the following conditions when measuring S-parameters:
- The test frequency
- The characteristic impedance (usually 50 Ω)
- The allocation of port numbers
- Other conditions, such as the bias current, temperature, and control voltage
Representing S-parameters
S-parameters are displayed as a  matrix, where
matrix, where 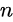 denotes the input port.
denotes the input port.
Thus, the S-matrix for a two-port network is written as:
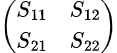
Where:
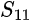 is input port reflection coefficient
is input port reflection coefficient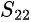 is the output port reflection coefficient
is the output port reflection coefficient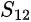 is the input port transmission coefficient (or “reverse voltage gain”)
is the input port transmission coefficient (or “reverse voltage gain”)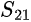 is the transmission coefficient (or “forward voltage gain”)
is the transmission coefficient (or “forward voltage gain”)
Note that diagonal parameters are termed “reflection coefficients” because signal inputs and outputs occur at a single port, while off-diagonal parameters are termed “transmission coefficients,” indicating inputs and outputs at different ports. This is similar for any 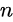 th-order matrix.
th-order matrix.
S-parameters may be plotted on a linear or polar diagram, in which each dot represents a test frequency.
S-parameters in RF Circuit Design
Engineers measure S-parameters to determine characteristics such as loss, gain, impedance, and voltage standing wave ratio (VSWR) in a high-frequency (RF or microwave) linear network. Various electrical standards, including 10 GbE, SATA, PCIe, and fiber channels all use S-parameters to formulate their testing compliance procedures.
Key applications include:
- Amplifier Design: In RF amplifier design, engineers rely on S-parameters to analyze gain, stability, and linearity to obtain maximum bandwidth and input/output matching outcomes.
- Filter Design: S-parameters help engineers assess the frequency response, insertion loss, return loss, and selectivity in high-pass, band-pass, low-pass, and band-stop filters.
- Frequency Response Characterization: Because S-parameters vary with applied frequencies, they can reveal the characteristic responses of RF circuits over a wide range of frequencies, allowing the characterization of bandwidth, resonance, parasitic influences, and other frequency-dependent responses.
- Transmission Response Characterization: S-parameters reveal how well RF circuits transfer power between ports, characterizing responses in loss, gain, and phase shift.
- Impedance Matching: By examining S-parameters (specifically reflection coefficients), engineers can achieve optimal impedance matching between circuit components and maximize power transfer between sources and loads.
- Interconnect Analysis: S-parameters help characterize crosstalk, signal integrity, impedance mismatches, and other effects in interconnects and transmission lines.
- Signal Integrity Analysis: Signal power may be negatively affected by attenuation, reflections, and impedance mismatches, which engineers can mitigate by examining the S-parameters in a network.
- Circuit Design: Engineers use S-parameters to evaluate different RF circuit configurations to optimize design specifications for gain, loss, power transfer, and impedance matching.
- Network Analysis: Engineers can analyze the performance of complex networks (such as phase shift, gain, and frequency response) by cascading the S-parameters of individual components.
Benefits of Using S-parameters
S-parameters provide engineers with valuable information concerning the performance of linear electrical networks, including RF circuits, amplifiers, and filters. This information includes:
- Details of signal magnitude, phase, reflection, and attenuation
- Locations of signal losses and impedance mismatches
- Transmission line parameters, such as R, L, C, G, TD, and Z0
Furthermore, S-parameters are easier to measure than Y- or Z-parameters at RF frequencies because they don’t require open or short circuits. They are also easily converted to other parameter formats, including ABCD parameters, H-parameters, T-parameters, Y-parameters, and Z-parameters, providing flexibility in circuit analysis and design.
S-parameters are also easily saved as Touchstone files (ASCII text files) that are readable by circuit simulation software.
Limitations of Using S-parameters
While using S-parameters has many advantages, there are a few limitations:
- S-parameters can only be used in frequency domain analysis (frequency response of signals) but cannot be used in time domain analysis (transient response of signals).
- When using S-parameters, it’s not possible to characterize networks in terms of voltage and current waves simultaneously. For this, engineers use ABCD parameters. Also, it’s easier to cascade ABCD parameters than it is S-parameters.
- Most silicon loads behave nonlinearly.
Digital circuits are largely governed by voltage thresholds, in which engineers need to understand the flow of electrical energy, therefore requiring time domain analysis. Time domain analysis is also important in circuit designs with antennas, in which engineers need to characterize reflections and stray signals.
Frequency domain analysis simplifies mathematical analysis and provides an intuitive understanding of system quality. Engineers use terms like gain, bandwidth, resonant frequency, and phase shift when they wish to reference the time-dependent elements of frequency characteristics.
Also, it is possible to convert signal information between the frequency and time domains using mathematical operators called transforms (e.g., Fourier transforms), although this may introduce errors.
Types of S-parameters
In the matrix model, a “black box” represents an electrical network containing interconnecting components — such as transistors, capacitors, resistors, and inductors — that interact with other circuits through various ports.
The network may contain any number of components, provided it behaves linearly when small incident signals are applied to it. It may also include typical communication systems components, such as attenuators, amplifiers, couplers, and filters, provided they are also operating linearly.
Small-Signal S-parameters
In the vast majority of cases, S-parameters apply to single-frequency, small-signal networks. In these networks, the signal is small enough that gain compression or other nonlinear effects are negligible. Thus, small-signal S-parameters are simply calculated as the voltage ratios of reflected and incident waves.
Linear networks include:
- Lossless networks that do not dissipate power, such that the sum of the incident powers equals the sum of reflected powers across all ports. This implies the S-parameter matrix is unitary.
- Lossy passive networks in which the sum of incident powers exceeds the sum of outgoing powers, meaning the network dissipates power.
- Reciprocal passive networks, composed solely of reciprocal materials that influence the transmitted signal. Cables, splitters, attenuators, and combiners are all examples of reciprocal networks. In this case, the S-parameter matrix is equal to its transpose, such that
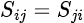
Large-Signal S-parameters
As the strength of the input signal increases, non-linear effects such as gain compression become noticeable. Therefore, large-signal S-parameters vary with input power levels. These are also called “power-dependent S-parameters.”
Engineers base their large-signal S-parameter measurements on a harmonic balance simulation of the network, which is a frequency-domain analysis method applied to nonlinear circuits. Large-signal S-parameters are also calculated as voltage ratios of reflected and incident waves.
Mixed-Mode S-parameters
Engineers frequently need to check S-parameter calculations against frequency versus gain plots or Smith charts. Hence, mixed-mode S-parameters are plotted. Engineers use these parameters to characterize near-end cross-talk (NEXT) and far-end cross-talk (FEXT) in differential networks.
Two-Port S-parameters
Engineers commonly use two-port S-parameters in network analysis, which also serve as the blueprint for higher-order S-parameter matrices in larger networks. The relationship between reflected and incident waves in two-port networks is given by:
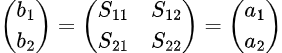
where 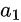 and
and 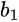 are the incident and reflected wave amplitudes, respectively, at port 1, and similarly for
are the incident and reflected wave amplitudes, respectively, at port 1, and similarly for 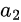 and
and 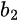 at port 2.
at port 2.
Engineers derive the following network properties from two-port S-parameter measurements:
- Insertion loss
- Input return loss
- Output return loss
- Scalar linear gain
- Complex linear gain
- Scalar logarithmic gain
- Reverse gain and reverse isolation
- Reflection coefficient
- Voltage standing wave ratio
Measuring Signal Integrity Using S-parameters
As noted previously, S-parameters help engineers describe the response of a general 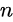 -port electrical network, in which signals are applied and reflected at any of the ports. Thus, a parameter
-port electrical network, in which signals are applied and reflected at any of the ports. Thus, a parameter 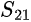 describes a network response at port 2 from an incident signal at port 1. S-parameters are commonly applied to one- and two-port networks.
describes a network response at port 2 from an incident signal at port 1. S-parameters are commonly applied to one- and two-port networks.
Three-port S-parameter measurements prove more challenging, although engineers can model them using specialized software. Also, multiport S-parameter measurements are readily available from device manufacturers, but engineers always need to check these measurements for accuracy.
Using Vector Network Analyzers (VNAs)
Signal integrity engineers routinely use vector network analyzers to assess the performances of RF and microwaves circuits over a range of operating conditions. As a result, they often de-embed, cascade, and visualize a significant amount of S-parameter data, performing a combination of theoretical analysis and experimentation. The process typically involves:
- A theoretical analysis of the circuit model or schematic, applying electromagnetic theory, transmission line theory, and circuit theory to derive mathematical equations
- Simulation of the circuit behavior with the help of specialized software (based on the derived equations) to extract S-parameters
- Experimentation with a vector network analyzer to extract S-parameter values over a range of frequencies
- De-embedding (subtracting) the S-parameter contributions of individual components from a circuit where required
During testing, engineers feed a known signal from a VNA source into a DUT in order to measure alterations to the signal as it traverses the DUT. These alterations are captured by a receiver (or a group of receivers) connected to the VNA.
A typical VNA setup includes:
- A sweep oscillator (usually a synthesizer)
- An information display unit
- Two or more ports (often connected to dual directional couplers and a complex ratio measuring device)
- RF cables
Optionally, a means of controlling bias voltage or current or a controller to store data may be included.
A vector network analyzer captures the frequency responses of a single component (or a group of components, either passive or active) in an RF network. It measures the power of a given signal, capturing its phase and amplitude.
Engineers may derive a range of device characteristics from these amplitude and phase measurements, including group delay, impedance, return, and insertion loss characteristics.
VNAs are single or multipath instruments comprising several ports, where stimuli may be applied at any of the ports, such that:
- A two-port, one path VNA returns reflected and transmitted signal values at input port 1 (
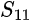 and
and 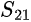 , respectively). However, the DUT must be reversed to obtain the opposite parameters at port 2 (
, respectively). However, the DUT must be reversed to obtain the opposite parameters at port 2 (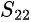 and
and 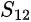 ).
). - A two-port, two-path VNA can also reverse the signal flow, meaning measurements may be performed in either direction to extract the reflection and transmission coefficients at any port.
Furthermore, the position of the reference plane, where calibrations are carried out, influences VNA measurements.
Measurement Errors
Sources of measurement errors include:
- Variations in frequency responses, caused by slight variations in the frequency responses of the VNA’s receivers
- Variations in port impedances, caused by slight differences between the characteristic reference impedance and the input impedance at the test port
- Errors in directionality, in which portions of incident and reflected waves impinge on each other, affecting measurements in either direction
- Errors in isolation, in which a small portion of the incident signal at one port may leak into the receiver channel of another port, resulting in crosstalk.
Visualizing S-parameters
Visualization forms an important first step in analyzing S-parameter data. Phase and amplitude data may be plotted in either Cartesian or polar coordinates. A Smith chart is a polar plot used in the analysis of matching networks.
Performing S-parameter calculations accurately requires a firm understanding of RF circuit theory, experience with simulation software, and access to reliable equipment.
Designing S-parameters in RF Circuits
Designing RF circuits is a complex task, involving multiple iterations. Accuracy, the complexity of the circuit, and the tools available determine the approach.
Following are the steps in a typical approach to designing S-parameters in a high-frequency RF circuit:
- Circuit Layout: In the circuit layout design, the engineer considers the topology of circuit components, transmission lines, and interconnects, paying attention to impedance matching and signal integrity.
- Component Selection: The engineer selects amplifiers, mixers, filters, and other components according to requirements, balancing characteristics in gain, power handling, frequency response, and others.
- Simulation and Optimization: The engineer programs a circuit model, interconnections and component properties, and other parameters into a specialized software tool to obtain simulated S-parameter values. They then fine-tune the inputs (such as the length of transmission lines) to reach optimal S-parameter values in bandwidth, gain, impedance matching, and others.
- Prototyping: Once desired parameters are obtained, the engineer builds a circuit prototype using a vector network analyzer to measure actual S-parameter values.
- Validation: As a final step in the process, the engineer may compare VNA S-parameter values with simulated ones. Any discrepancies will prompt them to refine the circuit design and component selection, repeating the process until measured and simulated S-matrices align.
About Ansys RaptorH Software
The shift from parallel to high-speed serial data transmission is giving rise to a range of new semiconductor design challenges. With data rates nearing the gigabit-per-second — pushing more bits through every interconnect — multiple serial links working in parallel will be needed, leading to high-frequency interconnect losses and increases in crosstalk.
Therefore, it becomes essential to characterize electromagnetic coupling in semiconductor chips.
Ansys Ansys RaptorH™ electromagnetic (EM) modeling software has been designed for the optimal configuration of semiconductor circuits, combining the Ansys HFSS™ engine with Ansys RaptorH software in one convenient package.
Supported by all major silicon foundries, RaptorH software’s high-speed distributed processing provides precise, silicon-proven S-parameter and RLCk modeling in minutes. Visit the dedicated Ansys RaptorH software page for further information.
∑_(i=1)^n I_i=0
Related Resources
Let’s Get Started
If you're facing engineering challenges, our team is here to assist. With a wealth of experience and a commitment to innovation, we invite you to reach out to us. Let's collaborate to turn your engineering obstacles into opportunities for growth and success. Contact us today to start the conversation.