-
-
Access Free Student Software
Ansys empowers the next generation of engineers
Students get free access to world-class simulation software.
-
Connect with Ansys Now!
Design your future
Connect with Ansys to explore how simulation can power your next breakthrough.
Countries & Regions
Free Trials
Products & Services
Learn
About
Back
Products & Services
Back
Learn
Ansys empowers the next generation of engineers
Students get free access to world-class simulation software.
Back
About
Design your future
Connect with Ansys to explore how simulation can power your next breakthrough.
Free Trials
TOPIC DETAILS
What is Nodal Analysis?
Nodal analysis is a method for calculating the voltage at the connections, called nodes, between components in an electric circuit. It is a fundamental part of circuit analysis for everything from a simple wired circuit connecting discrete components to complex semiconductor integrated circuits (ICs).
In a simple nodal analysis, each connection between components — the traces or wires — is referred to as a node. Kirchoff’s laws and Ohm’s law are used to write equations relating the resistance, current, and voltage of every conductive path leading to each node. The system of equations is then solved by hand or using linear algebra for the voltage drop at each node. For larger problems, software, usually in the form of a SPICE circuit simulator, is used to conduct nodal analysis.
The Fundamental Laws of Nodal Analysis
The nodal analysis method is based on the use of three fundamental laws:
1. Kirchhoff's Current Law (KCL)
The algebraic sum of all currents entering and exiting a node must equal zero.

Where I is current and n is the number of branches feeding into the node.
2. Kirchhoff's Voltage Law (KVL)
The algebraic sum of all potential differences (voltages) in a loop must equal zero.
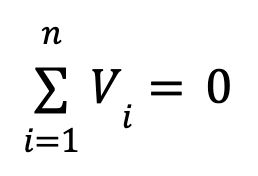
Where V is voltage and n is the number of places where voltage is measured around the loop.
3. Ohm’s Law
The electric current (I) through a conductor is equal to the voltage (V) across the conductor divided by the resistance (R) of the conductor.
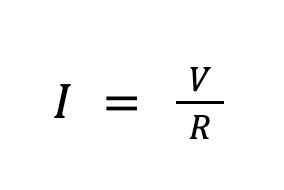
Nodal Analysis Terminology
For a nodal analysis, a circuit diagram is used to represent a network of the following items:
Reference node: A node in the circuit in which the voltage is known. This is usually a ground node, and the voltage is set to 0.
Nonreference node: any node in which the voltage is unknown
Voltage source: a component in the circuit in which the potential is changed by a known voltage
Current source: a component with a known current
Supernode: When a voltage source has two unknown voltages on either side, it can be turned into a supernode, in which the currents of the two nodes are combined into a single equation. A new equation for the supernode’s voltage-current relationship can then be written.
Component: An electronic device with a known relationship between voltage and current. For a resistor, that relationship is based on resistance. It is often expressed as admittance, or the inverse of resistance. For a capacitor, the relationship is dependent on the relationship between capacitance and change in voltage over time.
Modified nodal analysis: For more complex circuits, a simple nodal analysis may not be sufficient to find all of the unknown voltages. For cases in which a component’s current-voltage relationship is more complicated than Ohm’s law, a modified nodal analysis is performed.
Mesh analysis: If currents are not known, Kirchhoff's Voltage Law is used in what is called a mesh analysis to find the unknown branch currents.
Why Nodal Analysis is Important
Electronic circuits are designed to transfer electrical current to deliver power and a signal. Engineers who design circuits need to know that the electronics they define perform as expected. Nodal analysis is conducted to calculate node voltages and current flows for every portion of the circuit. Once these fundamental values are known, a more complex analysis can be done to understand signal integrity, heating, and overall power performance.
For PCB-level designs, nodal analysis can be used to understand the impact of the board’s topology, the effect of different components, and the overall distribution of power across conductance paths such as ground planes, traces, and vias.
For microchips of every kind, understanding power losses becomes even more important. The number of nodal equations can become significant because of the sheer number of nodes. Understanding and verifying the distribution of current, voltage, and power can only be accomplished through circuit analysis.
Calculating voltage drops is another common use for nodal analysis, especially in today’s complex semiconductor products. Any time the potential drops between nodes, heat is generated and power you may need somewhere else is lost. Nodal analysis tools are used on even the most complex semiconductors to any weaknesses in the circuit caused by unwanted or concentrated voltage drops.
Chip designers can use the tools to go beyond finding problems to enable what-if studies to optimize power and performance. Tools like Ansys RedHawk-SC™ power integrity signoff platform for digital and 3D-ICs run on large HPC cloud platforms to support large circuits with millions of components in the latest semiconductor architecture. Because this is such a trusted method, many major foundries certify RedHawk-SC software for signoff.
The Steps Used to Perform a Nodal Analysis
Whether done by hand or automated in software, a nodal analysis follows the procedure below:
1. Define Nodes
Capture all connected conductive segments in the circuits (the nodes). If solving by hand, draw the circuit and number the nodes. If using software, a list of all the nodes and their connectivity to components is created programmatically from a schematic.
2. Choose Ground Node
Select a node as the reference node and define its voltage as the ground voltage. This reduces the number of unknowns in the system by one. If you have n nodes, you then need to solve n-1 equations.
3. Create Variables
For each nonreference node in whch the voltage is unknown, assign a variable to signify the voltage of that node. The nodes with a known voltage do not need a variable.
4. Construct Node Equations
Step through each node with an unknown voltage and write the KCL equation for that node. This consists of adding together the calculated branch currents for each leg of the node and setting that sum to zero. The current between two nodes can be a known value if a current source sits between the nodes. It is the voltage difference between the nodes divided by the resistance between the nodes, or it can be a relationship between voltage change and capacitance for a capacitor. Other components may have more complex equations.
5. Join Nodes as Supernodes
Combine any voltage sources connecting two unknown voltages into supernodes with a single equation.
6. Assemble and Solve
Unless the circuit is small enough to solve by hand, the system of simultaneous equations can be rearranged into a square matrix consisting of n-1 columns and rows. Linear algebra numerical methods can then be used to solve for the unknown voltages.
Some Simple Examples of Nodal Analysis
Here is a simple example to better illustrate this process. Pictured below is a circuit with one current source, one voltage source of 10 volts, and two resistors. The voltage V1 is not known.
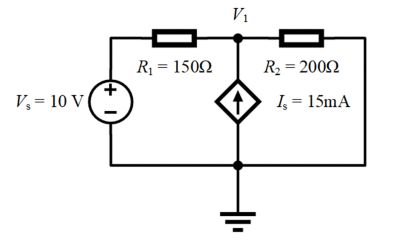
- V1 is the only unknown voltage. The other node is attached to ground and will be our reference point.
- The node V1 has three branch currents:
- The current through resistor R1: (V1 - Vs)/R1
- The current through resistor R2: (V1 - 0)/R2
- The current through current source Is: - Is
- By Kirchoff’s Current Law, we sum them and set them to 0:
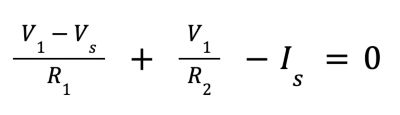
4. Rewrite in terms of V1:

Now let’s use the nodal analysis method to look at a circuit with a voltage source connected to two unknown voltages.
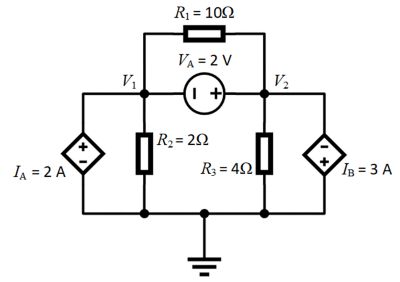
- V1 and V2 have an unknown nodal voltage. The other node is attached to ground and will be our reference node set to 0 volts. Also, VA is between V1 and V2, so it is a supernode.
- The node V1 has three branch currents:
- The current through resistor R1: (V1 - V2)/R1
- The current through resistor R2: (V1 - 0)/R2
- The current through current source IA: - IA or 2 amps
- The node V2 has four branch currents:
- The current through resistor R1: (V2 - V1)/R1
- The current through resistor R2: (V2 - 0)/R3
- The current through current source Ib: Ib or 2 amps
- The supernode equation for VA: V2 = V1 + VA
- By Kirchoff’s Current Law, we sum the current flows for node 1 and set them to 0:
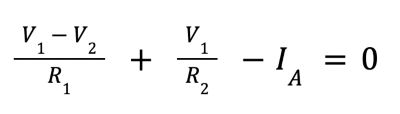
5. Rewrite in terms of V1:
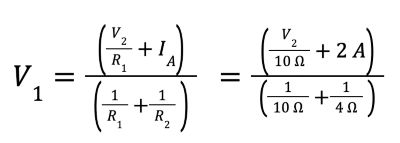
6. By Kirchoff’s Current Law, we sum the current flows for node 2 and set them to 0:
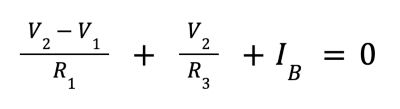
7. Rewrite in terms of V2.
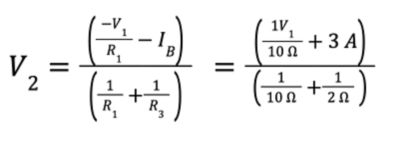
8. Using the supernode equation for V2 and solving the other two equations, we get V1 = -7.33 V and V2 = -5.33 V
Getting Started on Nodal Analysis of Complex Electrical Systems
Nodal analysis, usually in the form of a SPICE solver, is a fundamental step in characterizing the behavior of any electrical circuit. From simple circuits on a breadboard to the industry’s latest semiconductor with millions of transistors, engineers need to use tools like Ansys Totem™ power integrity signoff platform to not just calculate voltages, but also use that information to understand power noise and achieve reliability signoff for analog mixed-signal designs.
Ansys Twin Builder® software offers a full nodal analysis solver that can be combined with other reduced-order tools. With it, you can analyze your circuit and what it is attached to in your product, all in one interface.
Here are a few suggestions to make applying nodal analysis to complex electrical systems efficient and successful:
- Understand all the circuit elements in your design before constructing your nodal analysis model, including their electrical properties.
- Make sure that your assumptions about reference nodes are correct, that they are truly grounded, and that the voltage can’t float.
- Make sure you are using a tool that can read your ECAD data seamlessly and requires minimal user input to construct your circuit representation.
- Take the time to understand the basics of nodal analysis. Spend some time with tutorials that do simple circuit analysis related to the type of components you need to characterize.
- Use a software tool that does more than a nodal analysis. Work with a solution that treats the nodal analysis of a given circuit as a starting point for further simulations.
Related Resources
Let’s Get Started
If you're facing engineering challenges, our team is here to assist. With a wealth of experience and a commitment to innovation, we invite you to reach out to us. Let's collaborate to turn your engineering obstacles into opportunities for growth and success. Contact us today to start the conversation.