-
-
学生向け無料ソフトウェアにアクセス
Ansysは次世代の技術者を支援します
学生は、世界クラスのシミュレーションソフトウェアに無料でアクセスできます。
-
今すぐAnsysに接続!
未来をデザインする
Ansysに接続して、シミュレーションが次のブレークスルーにどのように貢献できるかを確認してください。
国および地域
無料トライアル
製品およびサービス
リソースとトレーニング
当社について
Back
製品およびサービス
トピックの詳細
陽解法動とは
陽解法動解析とは、非線形・動的挙動を表現する数値モデルを指し、陽的時間積分法を用いた有限要素法(FEM)を使用して、荷重に対する応答をより小さな時間増分で計算します。
陽的時間積分法は、短時間の時間依存挙動を示す非線形問題に最適です。陽解法動解析の一般的な適用例としては、落下試験、車両衝突、金属成形、材料破壊などが挙げられます。
有限要素法解析(FEM)シミュレーションでは、陰的時間積分法を使用することもできます。陽解法は、計算効率の高い多くの小さな時間ステップを用いるのに対し、陰解法はより少ない大きな時間ステップを使用します。計算コストも非常に高くなります。どちらの手法が最適かは、システムの全体的な非線形性と事象の持続時間によって決まります。
有限要素法
FEMは、常微分方程式または偏微分方程式(PDE)を解くために用いられる数学的手法です。物理システムのシミュレーションでは、領域を離散的なチャンク(有限要素)に分割してから、ソフトウェアによって各要素にPDEを適用します。その後、ソフトウェアが方程式を組み立て、数値ソルバーを使用して未知数を求めます。FEMを用いて物理システムをモデル化することを有限要素法解析(FEA)と呼びます。
非線形
FEAにおける「非線形」とは、代表的な方程式が線形でない挙動を指します。典型的な非線形挙動には、非線形材料モデル、大変形、境界条件、動的荷重、複雑な接触、材料破壊などがあります。
動力学シミュレーション
物体の完全な運動方程式は以下の通りです。
力 =(質量 × 加速度)+(減衰 × 速度)+(剛性 × 変位)
加速度がほとんどない、あるいは速度が一定の場合、その問題は静的問題と呼ばれます。この場合、FEAソルバーは、力と変位の未知の値を求めるだけで済み、時間は関与しません。しかし、速度が変化する場合には、時間の経過とともに変化するため、その問題は動的問題として扱われます。
陽的時間積分法
動的事象を表す有限要素モデルにおけるPDEは、所定の時間ステップで解かれます。したがって、ソフトウェアはPDEを時間的に積分する必要があります。この積分結果が、現在の時間ステップでの既知量から次の時間ステップでの値を陽的に計算する方程式になるため、この手法は「陽的」と呼ばれます。FEAで用いられるもう1つの手法である陰的時間積分法は、次の時間ステップで求めたい値が、既知量と未知量の両方を含む方程式を通じて間接的にのみ定義されることから、「陰的」と呼ばれます。この場合、ソルバーは線形代数を用いて陰的な未知量を計算します。
陽解法の1つである前進オイラー法は、現在の時間ステップでの量のみを関数とする方程式をもたらします。
$$y_{k+1} = y_k - \Delta t \, y_k^2 $$
陽解法動解析の重要な側面
シミュレーションソフトウェアで陽解法動解析手法を使用する場合、シミュレーション初心者も経験豊富なエンジニアも、この手法が採用する数学的アルゴリズムによって決まるいくつかの重要な側面を理解しておく必要があります。
臨界時間ステップと波動伝搬時間
考慮すべき最も重要な情報は、陽解法動解析手法が現在の時間ステップの直後の時間ステップを解くという点です。このソルバーは時間ステップでのひずみの変化を計算するため、時間ステップサイズは、モデル内の最小要素をひずみ波が通過するのにかかる時間に制限されます。この制限は臨界時間ステップと呼ばれ、波動伝搬時間は材料中の音速によって決まります。材料が剛性材料で、要素のサイズが小さい場合、臨界時間ステップは通常、数ミリ秒程度になります。
非線形挙動
次にエンジニアが理解しておくべき点は、陽解法動解析が捉えることのできる各種の非線形挙動です。極めて小さな時間ステップを使用する陽的手法では、その小さなステップで計算される値の変化を線形として扱うことができます。
FEAシミュレーションにおけるほとんどの非線形挙動は、以下のいずれかのカテゴリーに分類されます。
1.非線形材料
非線形材料は、荷重や時間の経過によって非線形的に変化する特性を有します。ほとんどの解析タイプにおいて最も一般的な材料非線形性の例は塑性です。特に材料剛性が低下するより高いレベルの塑性に対する収束を陰解法で判定するのは困難なことがあります。塑性と密接に関連する特性には、ひずみ速度依存性(剛性など)があります。材料非線形性のもう1つの例として、相変化や材料破壊によってよく引き起こされる、材料特性(特に剛性)の急激な変化が挙げられます。
2.非線形ジオメトリ
非線形ジオメトリの挙動の最も一般的な例は、大変形です。この場合、線形静的解析で使用される、小ひずみ速度の定式化はもはや有効ではありません。もう1つの例は、物体の重心が時間とともに移動したり、物体が一点を中心に回転したりする剛体運動です。
3.非線形境界条件および荷重
時間ステップに対して荷重が急激に変化する場合、陰解法解析では収束が困難になります。この荷重は、印加される荷重だけでなく、2つの物体間の接触を通じて伝わる荷重の場合もあります。
こうした非線形性は、多くの場合、高速で短時間の事象で現れます。陽的時間積分法で使用される小さな時間ステップにより、こうした変化をステップ間で線形として近似することができます。また、塑性時や材料破壊時に非線形システムを平衡状態に保つ内部力をソルバーが計算することも可能になります。
集中質量近似
動的問題を解くことができる陽的時間積分法のもう1つの重要な側面は、各要素の節点質量を集中質量として表現できることです。これにより、単一の対角成分を持つ質量行列が生成されるため、モデルの慣性値を計算するために必要な行列の逆行列計算が極めて容易になります。
準静的構造解析
システムの慣性効果が無視できるほど小さく、システムが本質的に常に平衡状態に保たれる場合、この解析は動的構造解析のサブセットである準静的構造解析と呼ばれます。このような挙動の好例が金属成形です。これは、材料特性(特に塑性)が時間依存性を持つという点で動的ですが、金属の慣性が塑性変形に影響を与えることはありません。
陰解法動とは
陽解法動解析について語る上で、陰解法動解析を避けて通ることはできません。その名称が示す通り、陰解法動解析は陰的時間積分法を用いるFEAシミュレーション手法です。陽解法動解析と同様に、陰解法動解析も、複数の時間ステップにわたって運動方程式全体を時間的に計算します。
陰的積分法の方程式には、現在の時間ステップと次の時間ステップの両方の値が含まれます。陰的シミュレーションソフトウェアツールでは、ソルバーが後退オイラー法を用いて、現在の時間ステップ(k)と次の時間ステップを関数とする、次の時間ステップでの値を求める方程式を導出します。
$$y_{k+1} = \frac{-1 + \sqrt{1 + 4 \Delta t y_k}}{2 \Delta t} $$
陰解法と陽解法の違い
構造解析では、両方の積分法が動的シミュレーションと準静的シミュレーションに用いられます。導入部で述べたように、主な違いは、陽解法でPDEを積分すると、結果として得られる方程式によって解が完全に定義されるのに対し、陰解法では、未知の値が暗黙的に含まれているため、アルゴリズムが解を求めるには線形代数を用いる必要がある点にあります。
実務的な観点からすると、これにより以下のような違いが生じます。
| 陰解法 | 陽解法 | |
| 時間ステップサイズ | 荷重の変化を捉え、非線形計算の収束を促進するために、ユーザーが設定する。時間ステップが大きいため、非常に少ないステップ数で済む。 | メッシュ内の最小要素を波動が伝搬する時間によって設定される。時間ステップサイズは数ミリ秒程度であり、短時間でも多くのステップを要する。 |
| ステップごとの計算サイクル数 | 連立方程式の完全解が得られる。非線形計算の収束が必要な場合には、時間ステップごとに複数の計算を実行する。 | 各ステップで非常に効率的な陽解法を用いており、集中質量行列の逆行列も容易に計算できる。 |
| メモリ必要量 | 陰的積分法と完全質量行列には、陽解法よりも大量のメモリが必要である。 | 陽的積分法と集中質量定式化は、陰解法に比べてはるかに少ないメモリで済む。 |
| 収束 | 非線形計算においては、平衡を確立するために、各時間ステップで収束を達成しなければならない。 | 小さな時間ステップでは線形仮定が成立するため、収束計算は不要である。 |
| 平衡 | 必要 | 不要 |
| 計算リソースに対するメッシュ数の感度 | 問題に依存する(結果として得られる行列の帯域幅が計算時間に影響を与えるため)。 | 要素数に線形的に依存する。 |
| 要素サイズの感度 | 実行時間は個々の要素サイズにはあまり依存しない。 | 最小要素サイズに線形的に依存する。最小要素サイズを半分にすると、実行時間が倍増する。 |
| 接触 | 力の平衡が達成されるまで反復計算が必要である。急激な接触変化により、解が発散する可能性がある。 | 反復計算は不要。急激な接触変化に適切に対応する。 |
| 材料破壊 | 要素の剛性や要素間の接続を除去すると、収束問題が発生する可能性があり、アダプティブメッシングが必要になることが多い。 | 時間ステップが小さいため、スムーズに対応できる。 |
| 材料の非線形性 | 材料特性の急激な変化や低い剛性は、平衡問題を引き起こし、その結果、収束問題を生じさせる可能性がある。 | 小さな時間ステップでは、所定の時間ステップ内で線形処理を行うことができる。 |
陽解法動解析シミュレーションの例
小さな時間ステップサイズと集中質量定式化を使用する陽解法動解析は、大きな非線形性を伴う短時間の事象に最適です。平衡問題が生じる長時間の準静的事象に関しては、陰解法解析よりもこの手法が選択されることがあります。
さまざまな業界において、Ansysの陽解法動解析ソリューション(Ansys LS-DYNAなど)を活用することで、高度で複雑な非線形構造シミュレーションに関する有用な情報を迅速に得ることができます。以下に、一般的な適用例をいくつか挙げます。
落下試験
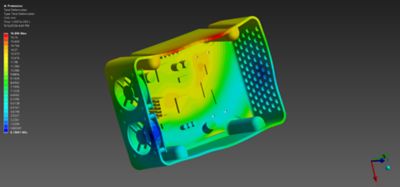
コンシューマ向け製品と産業用製品はいずれも、輸送中や使用中に起こり得る一定の高さからの落下に耐えなければならないため、エンジニアは業界標準の落下試験を用いて、製品が十分なロバスト性を有しているかどうかを確認しています。しかし、実機試験には費用がかかり、実際のハードウェアも必要です。Ansys Workbenchプラットフォームを介してコンピュータ支援設計(CAD)モデルとリンクさせることができるLS-DYNAのようなツールを使用すれば、コストを削減するとともに、仮想落下試験を製品開発プロセスの早期かつ低コストの段階で行うこともできます。
車両衝突

自動車衝突解析およびシミュレーションは、陽解法動解析シミュレーションのあらゆる適用例の中で最も多くの人々に影響を与え、無数の命を救ってきたと考えられます。車両が固体の物体や他の車両に衝突すると、短時間で金属構造が圧壊し、破壊されます。これは陽解法動解析に最も適した適用例と言えます。そのため、どの自動車メーカーもLS-DYNAや類似のツールを用いて、車両全体、シートベルトシステム、エアバッグ、およびバッテリパックのシミュレーションを実施しています。
人体への衝撃

短時間に物体に力を加える事象は、製品や機械だけでなく人体にも影響を及ぼします。このため、エンジニアはAnsys Hansモデルなどの高精度な人体構造モデルを陽解法動解析シミュレーションに組み込んでいます。もはや形状や質量を表す単なるダミーではない詳細な人体構造モデルは、レーシングカーの衝突から頭部へのパンチに至るまで、さまざまな状況下で人体構造の各部位にかかる荷重や損傷領域を示すことができます。
心臓のシミュレーション
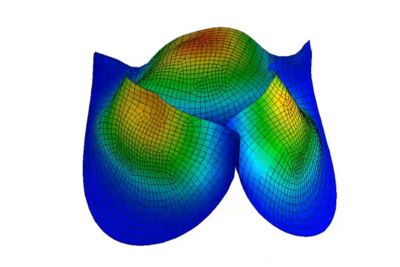
人間の心臓は、構造に駆動されるマルチフィジックスの最も複雑な例の1つです。電気インパルスが筋肉組織に大きな変形を引き起こすと、これによって弁が開閉し、血液が押し出されたり、引き込まれたりします。研究者やエンジニアは、LS-DYNAなどの真のマルチフィジックス陽解法動解析ツールを用いて、血流などの現象の数値流体力学(CFD)を含む、こうした動的な相互作用をモデル化しています。
金属成形
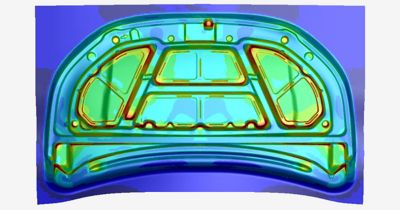
人類は青銅器時代から金属をたたいて成形してきましたが、現代では、陽解法動解析シミュレーションを用いて、このプロセスを最適化しています。剛体工具が薄板金属を曲げて形成する成形段階は、FEAにおける陽解法動解析手法の最も適した適用例です。一方、スプリングバックや熱処理といったプロセスは、時間がかかるため、陰解法による解析を行うのがベストです。このため、エンジニアは、LS-DYNAなどの陽解法ツールから、同一ツールの陰解法ソルバーへ、あるいは構造FEAソフトウェアであるAnsys Mechanicalなどの別のソフトウェアへとシミュレーションを移行させることができるワークフローを活用しています。
はんだのリフロー
年間数百万個ものマイクロチップを生産している半導体メーカーは、これらのチップを物理的かつ電気的に接続するために微小なはんだボールを使用しています。このはんだボールの品質は、ほぼすべてのエレクトロニクス製品の性能、冷却、ロバスト性に影響を及ぼします。陽解法動解析シミュレーションは、溶融して表面張力下で流れ、その後固化するはんだの非常に非線形な材料挙動に対応することができます。
ここでは、陽解法動解析シミュレーションソフトウェアツールのいくつかの一般的な適用例を挙げたに過ぎません。その他にも、以下のような適用例があります。
- 防衛分野、特に弾薬や装甲に関連する分野。この種の課題には、Ansys Autodynが特に適している。
- フライス加工や旋削などの機械加工プロセスにおける工具設計と機械加工速度の最適化
- 車両の操縦に伴う容器内のスロッシング挙動
- 臨界荷重下における構造物の座屈
- 短時間の動的事象にさらされるスポーツ用品
ソルバーの性能、ユーザーインターフェース、計算能力の向上により、陽解法動解析の使用が大幅に拡大しました。この手法は、ハイエンドの航空宇宙・防衛(A&D)分野に限定されていたものの、現在では自動車設計をはじめとする多くの分野で活用されています。特に、従来の陰的時間積分ソルバーでは対応が困難な、短時間ながら強烈な荷重や非線形性を伴う状況で真価を発揮します。
また、Ansysなどの主要なベンダーでは、エンジニアが熟練して設計を推進し、性能、安全性、耐久性の向上を実現できるよう支援するために、広範なトレーニング、サポート、および事例を提供しています。
関連リソース
さあ、始めましょう
エンジニアリング課題に直面している場合は、当社のチームが支援します。豊富な経験と革新へのコミットメントを持つ当社に、ぜひご連絡ください。協力して、エンジニアリングの障害を成長と成功の機会に変えましょう。ぜひ今すぐお問い合わせください。