什麼是顯式動力學?
顯式動力學是指呈現非線性動態行為的數值模型,這些模型使用有限元素法 (FEM) 搭配顯式時間積分法,計算系統在短時間間隔下,對於施加負載的反應。
顯式時間積分法最適合處理在短時間內發生時間相關行為的非線性問題。顯式動力學分析的典型應用,包括落摔測試、車輛碰撞、金屬成形及材料失效。
有限元素分析 (FEA) 模擬也可以使用隱式時間積分法。顯式方法涵蓋大量的小型時間步階,計算效率優異;隱式方法則採用為數較少卻較為龐大的時間步階。這些計算在運算資源上的消耗也大幅增加。最合適的方法取決於系統的整體非線性程度,以及事件的持續時間長短。
有限元素法
有限元素法 (FEM) 是用於求解普通微分方程式或偏微分方程式 (PDE) 的數學方法。在模擬物理系統時,使用者會將研究區域細分為離散區塊,也就是有限元素,並由軟體對每個元素套用 PDE。接著,這個工具會組合這些方程式,並使用數值求解器來求解未知答案。使用 FEM 建立物理系統模型,則被稱為有限元素分析 (FEA)。
非線性
在 FEA 所稱的「非線性」,是指代表方程式而非線性的行為。典型的非線性行為包括:非線性材料模型、大變形、邊界條件、動態負載、複雜接觸及材料失效。
動力學模擬
物體的完整運動方程式為:
力=(質量x加速度)+(阻尼x速度)+(剛度x位移)
當加速度極小或速度保持不變時,此問題可稱為靜態問題。在這種情況下,FEA 求解器僅需計算力與位移的未知值,無須考慮時間。然而,速度若發生變化,此問題即稱為動態問題,因為會隨著時間而改變。
顯式時間積分法
在表示動態事件的有限元素模型中,PDE 是在已知時間步階下求解。所以,軟體必須隨時間對 PDE 進行積分。我們將顯式動力學方法稱為「顯式」,是因為積分的結果是一個方程式,它會利用當前步階的已知量,明確算出下一個時間步階值。在 FEA 中使用的另一種方法為隱式時間積分法,這裡之所以稱為「隱式」,是因為下一時間步階的所需值,僅能透過涉及已知與未知量的方程式間接定義。在這種情況下,求解器會使用線性代數,計算隱含的未知數。
顯式方法的例子之一是前向歐拉法,其結果是得出僅取決於當前時間步階的方程式:
$$y_{k+1} = y_k - \Delta t \, y_k^2 $$
顯式動力學分析的關鍵面向
在模擬軟體使用顯式動力學解法時,無論是初學者還是老練的工程師,都需要注意該方法的一些重要面向,這些面向取決於其所用的數學演算法。
臨界時間步階與波傳播時間
最為重要的一點是,顯式解法只會解出當前時間步階之後的下一個時間步階。由於求解器會計算應變在時間步階中的變化,時間步階大小於是受到限制,其上限為應變波通過模型中最小元素所需的時間。這個限制稱為臨界時間步階,聲波在材料中的傳播速度,則決定了波傳播時間。對於剛性材料與小型元素尺寸,臨界時間步階通常為毫秒等級。
非線性行為
工程師需要注意的下一個層面是顯式動力學所能捕捉的不同非線性行為類型。由於顯式方法採用微小時間步階,便能將計算值在該微小步階中的變化視為線性。
工程師通常將 FEA 模擬中的大多數非線性行為,歸類為以下幾種:
1.非線性材料
非線性材料的特性會隨著負載或時間,以非線性的方式改變。可說在任何分析類型中,最為常見的材料非線性形式是塑性。隱式方法在處理高度塑性時,欲決定收斂性可能並非易事,尤其是材料剛度降低的情況。與塑性密切相關的還有依應變率而異的特性,例如剛度。另一種材料非線性形式,則涉及到材料特性的突然變化,特別是剛度,這通常相變或材料失效所致。
2.非線性幾何
在非線性幾何行為中,最為常見的形式是大變形。這是線性靜態分析中使用的小規模應變率公式不再適用的情況。另一種形式是剛體運動,即是物體的質心隨時間移動,或物體環繞著某一點旋轉。
3.非線性邊界條件與負載
當負載的變化快於時間步階時,隱式分析會變得難以收斂。這可能是施加的負載,或是兩個物體接觸所傳遞的負載。
高速且時間短暫的事件,常會展現出這些類型的非線性行為。顯式時間積分法所用的微小時間步階,可讓這些變化在相鄰時間步階之間幾近為線性。這些時間步階也讓求解器能算出在塑性或材料失效期間,讓非線性系統得以保持平衡的內力。
集中質量近似法
顯式時間積分方法在解決動態問題時的另一個關鍵面向,即是能以集中質量呈現每個元素的節點質量。如此一來,會產生只有單一對角線的質量矩陣,因此讓計算模型慣性值所需的矩陣反轉變得簡單。
準靜態結構分析
當系統中的慣性效應小到可忽略,並且系統在整個期間基本上保持平衡時,就會出現動態結構分析的子集。金屬成形即是此行為的典型例子。這種行為具有動態性,因為材料特性 (尤其是塑性) 會隨著時間變化,但金屬慣性不影響其塑性變形。
什麼是隱式動力學?
欲闡述顯式動力學,就必須討論隱式動力學。顧名思義,隱式動力學是使用隱式時間積分法的 FEA 模擬方法。如同顯式動力學,隱式動力學仍會利用多個時間步階,隨著時間求解完整的運動方程式。
隱式積分法的方程式,與當前時間步階與下一時間步階的數值密切相關。在隱式模擬軟體工具中,求解器會使用後向歐拉法得出方程式,以計算下一時間步階的數值,這些數值是當前步階 (k) 與下一步階的函數:
$$y_{k+1} = \frac{-1 + \sqrt{1 + 4 \Delta t y_k}}{2 \Delta t} $$
隱式方法與顯式方法的差異
工程師在結構分析中,會使用兩種積分法以進行動態與準靜態模擬。如前言所述,主要差異在於當 PDE 使用顯式方法進行積分時,該解答完全由得出的方程式加以定義。至於在隱式方法,未知數則是間接定義,所以演算法必須使用線性代數求解。
從現實世界的務實角度來看,此情況會導致以下差異:
| 隱式方法 | 顯式方法 | |
| 時間步階大小 | 由使用者設定,用於捕捉負載變化,並協助非線性計算收斂。時間步階龐大,所需時間步階數量甚少。 | 依穿越網格內最小元素的波傳播時間加以設定。時間步階大小約為毫秒,即使為時甚短也需要許多步階數。 |
| 計算每步週期數 | 聯立方程式的完整解法。若需要非線性計算需要收斂,每個時間步階可能會進行多次求解。 | 每個步階使用效率優異的顯式解法,並透過可簡單反轉的集中質量進行計算。 |
| 記憶體需求 | 隱式積分法與完整質量矩陣所需的記憶體,顯然多於顯式方法。 | 顯式積分法與集中質量公式所需的記憶體,遠少於隱式方法。 |
| 收斂 | 非線性計算為了建立平衡,必須在每個時間步階達成收斂。 | 不需要,因為微小時間步階允許假設為線性。 |
| 平衡 | 需求 | 不需要 |
| 網格數對計算資源的靈敏度 | 依問題而定,因為矩陣頻寬會影響求解時間。 | 與元素數量呈線性關係。 |
| 元素大小靈敏度 | 執行時間與單一元素的大小較為無關。 | 與最小元素大小成線性關係。最小元素尺寸減半,執行時間會加倍。 |
| 接觸 | 必須迭代直至達成力的平衡。若突然發生接觸變化,解法可能出現發散。 | 無須迭代。能妥善處理突然發生的接觸變化。 |
| 材料失效 | 移除元素剛度或元素間的連接,可能會導致收斂問題,通常需要用到自適應網格。 | 由於時間步階甚小,所以能順利處理。 |
| 材料非線性 | 特性突然變化與低剛度可能導致平衡問題,進而形成收斂問題。 | 使用微小時間步階,便能在已知時間步階內進行線性處理。 |
顯式動力學模擬範例
顯式動力學分析使用微小時間步階和集中質量公式,非常適合處理具顯著非線性的短時間事件。使用者可能會選用此方法取代隱式分析,以處理出現平衡問題的長時間準靜態事件。
工程師可使用 Ansys 顯式動力學解決方案,例如 Ansys LS-DYNA 軟體,跨產業快速產生高度複雜、非線性結構模擬的實用資訊。以下列出了一些較為常見的應用。
落摔測試
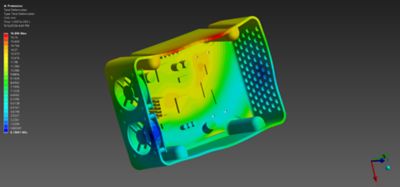
消費性產品或工業產品,在運輸與使用過程中,都需要能承受從合理高度掉落的衝擊,所以工程師會採用業界標準進行落摔測試,確保產品相當堅固耐用。但是,進行實體測試的費用昂貴,也需要用到實際的硬體設備。使用類似 LS-DYNA 軟體的工具,能透過 Ansys Workbench 平台,連接電腦輔助設計 (CAD) 模型以降低成本,並將虛擬落摔測試提前至產品開發過程中成本較低的初期階段進行。
車輛撞擊


施力至物體的短時間事件,不僅發生在產品與機械上,也會影響到人體。為此,工程師會在顯式動力學模擬中,放入如 Ansys Hans 模型的高傳真度人體結構模型。詳盡的人體結構模型不再是僅呈現形狀和質量的假人,而是可以在各種情境下 (從賽車碰撞到頭部撞擊),表示人體任一部位承受的負載與受傷部位。
心臟模擬
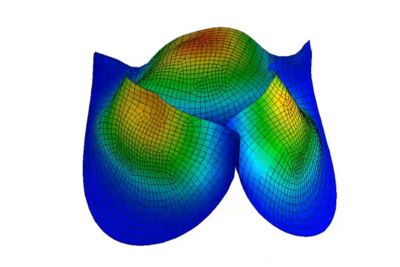
人體心臟是結構驅動多物理場中最複雜的典型例子之一。電脈衝會觸發肌肉組織大變形,進而推動血液經由閥門開啟與關閉而流動。研究人員與工程師會針對這種動態交互作用進行建模,其中包括血液流動等部分的計算流體力學 (CFD),並使用類似 LS-DYNA 軟體的真正多物理顯式動力學工具進行模擬。
金屬成形
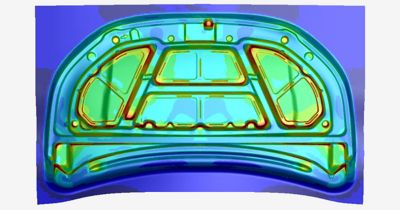
自青銅時代起,人類就一直敲打金屬塑形,但是到了矽時代,我們則使用顯式動力學模擬進行製程最佳化。在成形階段中,剛性工具會彎曲且塑形金屬薄板,這是 FEA 中顯式動力學方法的理想應用。相較之下,回彈與熱處理等製程的持續時間較長,較適合以隱式分析解決。因此,工程師可以用一個工作流程,將模擬從 LS-DYNA 軟體一類的顯式工具,轉移至同一工具的隱式求解器,或是轉移至另一款像是 Ansys Mechanical 結構 FEA 的軟體應用程式。
焊料回流
半導體製造商每年生產數百萬個微晶片,這些晶片使用細小焊料球進行物理與電氣連接。這些焊料球的品質,會影響幾乎每件電子產品的效能、散熱與可靠性。顯式動力學模擬能在焊料熔化、承受表面張力作用流動,然後凝固時,處理焊料的高度非線性材料行為。
這些只不過是顯式動力學軟體工具的幾件常見應用。其他用途包括:
- 國防應用,尤其涉及彈藥與裝甲的範疇時。Ansys Autodyn 軟體是特別適合處理此類問題的工具。
- 銑削與車削等加工製程,用於刀具設計與加工速度最佳化
- 操作車輛時,容器內液體的晃動行為
- 結構在承受臨界負載下的屈曲現象
- 承受短暫動態事件的運動用品
求解器功能、使用者介面與運算能力的改善,大幅擴展了顯式動力學的應用領域。這種方法在過去僅限於高階航太與國防 (A&D) 應用,如今已常見於汽車設計與許多其他領域。此法對於短暫而密集的負載,或是傳統隱式時間積分求解器難以處理的非線性情況甚具價值。
像 Ansys 等領導廠商,亦有提供廣泛的訓練、支援與範例,以協助工程師熟練運用並推動其設計,進而提升效能、增進安全性且改善耐用性。
相關資源
讓我們開始吧
如果您面臨工程挑戰,我們的團隊將隨時為您提供協助。憑藉豐富的經驗和對創新的承諾,我們邀請您與我們聯絡。讓我們共同合作,將您的工程障礙轉化為成長和成功的機會。立即與我們聯絡,開始對話。