-
-
Kostenlose Software für Studierende
Ansys unterstützt die nächste Generation von Ingenieur*innen
Studenten erhalten kostenlosen Zugang zu erstklassiger Simulationssoftware.
-
Verbinden Sie sich jetzt mit Ansys!
Gestalten Sie Ihre Zukunft
Stellen Sie eine Verbindung mit Ansys her, um zu erfahren, wie Simulation Ihren nächsten Durchbruch vorantreiben kann.
Länder und Regionen
Kostenlose Demoversionen
Produkte & Dienstleistungen
Lernportal
Über das Unternehmen
Back
Produkte & Dienstleistungen
Back
Lernportal
Ansys unterstützt die nächste Generation von Ingenieur*innen
Studenten erhalten kostenlosen Zugang zu erstklassiger Simulationssoftware.
Back
Über das Unternehmen
Gestalten Sie Ihre Zukunft
Stellen Sie eine Verbindung mit Ansys her, um zu erfahren, wie Simulation Ihren nächsten Durchbruch vorantreiben kann.
Kostenlose Demoversionen
THEMENDETAILS
Was ist explizite Dynamik?
Explizite Dynamik bezeichnet die numerischen Modelle, die nichtlineares, dynamisches Verhalten darstellen, die die Finite Elemente Methode (FEM) mit einem expliziten Zeitintegrationsansatz verwenden, um die Reaktion auf angewendete Lasten über kleine Zeitinkremente zu berechnen.
Explizite Zeitintegration eignet sich am besten für nichtlineare Probleme, die zeitabhängiges Verhalten über kurze Zeiträume hinweg erleben. Typische Anwendungen für "Explizite Dynamik"-Analysen umfassen Falltests, Fahrzeugunfälle, Metallformung und Materialversagen.
Die Simulation mit Finite Elemente Analyse (FEA) kann auch einen impliziten Zeitintegrationsansatz verwenden. Der explizite Ansatz umfasst viele kleine Zeitschritte mit effizienten Berechnungen, aber die implizite Methode benötigt weniger, größere Zeitschritte. Die Berechnungen sind ebenfalls wesentlich rechenintensiver. Welcher Ansatz am besten ist, hängt von der Gesamt-Nichtlinearität des Systems und der Dauer des Ereignisses ab.
Finite Elemente Methode
FEM ist eine mathematische Methode zur Lösung gewöhnlicher oder partieller Differentialgleichungen (PDG). Bei der Simulation physischer Systeme teilen Benutzende die Domäne in diskrete Blöcke auf, die als finite Elemente bezeichnet werden, und die Software wendet PDG auf jedes Element an. Das Tool fügt dann die Gleichungen zusammen, und numerische Solver werden verwendet, um die Unbekannten zu berechnen. Die Verwendung von FEM zur Modellierung physikalischer Systeme wird als Finite Elemente Analyse (FEA) bezeichnet.
Nichtlinear
In FEA bezieht sich "nichtlinear" auf Verhalten, bei dem die Repräsentantengleichung nicht linear ist. Typisches nichtlineares Verhalten umfasst nichtlineare Materialmodelle, große Deformationen, Randbedingungen, dynamische Belastung, komplexen Kontakt und Materialversagen.
Dynamiksimulation
Die vollständige Bewegungsgleichung für ein Objekt lautet:
Kraft = (Masse x Beschleunigung) + (Dämpfung x Geschwindigkeit) + (Steifigkeit x Verformung)
Bei minimaler Beschleunigung oder konstanter Geschwindigkeit kann ein Problem als statisch bezeichnet werden. In diesem Szenario muss ein FEA-Solver nur die unbekannten Werte für Kraft und Verformung bestimmen. Zeit spielt keine Rolle. Wenn sich jedoch die Geschwindigkeit ändert, wird das Problem als dynamisch bezeichnet, da es im Laufe der Zeit Änderungen gibt.
Explizite Zeitintegrationsmethode
Die PDG in einem Finite-Elemente-Modell, das dynamische Ereignisse darstellt, werden zu einem bestimmten Zeitschritt gelöst. Daher muss die Software die PDG im Laufe der Zeit integrieren. Der Ansatz der expliziten Dynamik wird "explizit" genannt, weil das Ergebnis der Integration eine Gleichung ist, die explizit den Wert im nächsten Zeitschritt für im aktuellen Schritt bekannte Größen berechnet. Die andere bei der FEA verwendete Methode, die implizite Zeitintegration, wird als "implizit" bezeichnet, da der gewünschte Wert beim nächsten Zeitschritt nur indirekt durch eine Gleichung definiert wird, die sowohl bekannte als auch unbekannte Größen umfasst. In diesem Fall verwendet der Solver lineare Algebra, um die implizierten Unbekannten zu berechnen.
Ein Beispiel für die explizite Methode, das Euler-Vorwärts-Verfahren, führt zu einer Gleichung, die nur eine Funktion des aktuellen Zeitschritts ist:
$$y_{k+1} = y_k - \Delta t \, y_k^2 $$
Schlüsselaspekte der "Explizite Dynamik"-Analyse
Bei der Verwendung der Lösungsmethode mit expliziter Dynamik in Simulationssoftware sollten sowohl Simulationsanfänger*innen als auch erfahrene Techniker*innen einige wichtige Aspekte der Methodik kennen, die durch mathematische Algorithmen bestimmt werden, die der Ansatz verwendet.
Kritischer Zeitschritt und Wellenausbreitungsdauer
Man muss dabei unbedingt bedenken, dass die explizite Lösung für den Zeitschritt direkt nach dem aktuellen Zeitschritt berechnet wird. Da der Solver berechnet, wie sich die Dehnung im Zeitschritt ändert, ist die Größe des Zeitschritts auf die Dauer beschränkt, die eine Dehnungswelle benötigt, um das kleinste Element im Modell zu durchqueren. Diese Beschränkung wird als kritischer Zeitschritt bezeichnet. Die Geschwindigkeit, mit der Schall durch das Material wandert, bestimmt die Wellenausbreitungsdauer. Bei steifen Materialien und kleinen Elementgrößen liegt der kritische Zeitschritt in der Regel im Bereich von Millisekunden.
Nichtlineares Verhalten
Der nächste Aspekt, der Techniker*innen bewusst sein sollte, sind die verschiedenen Arten nichtlinearen Verhaltens, die explizite Dynamik erfassen kann. Da der explizite Ansatz so kleine Zeitschritte verwendet, kann er die Änderung eines berechneten Werts über diesen kleinen Schritt als linear behandeln.
Techniker*innen ordnen das meiste nichtlineare Verhalten bei einer FEA-Simulation nach den folgenden Kategorien:
1. Nichtlineare Materialien
Nichtlineare Materialien haben Eigenschaften, die sich aufgrund von Belastung oder Zeit nichtlinear ändern. Die häufigste Form von Nichtlinearität bei Material ist bei fast allen Analysetypen die Plastizität. Der implizite Ansatz kann Probleme bei der Bestimmung der Konvergenz für höhere Plastizitätsstufen haben, insbesondere wenn die Materialsteifigkeit abnimmt. Eng mit der Plastizität verbunden sind von der Dehnungsrate abhängige Eigenschaften wie Steifigkeit. Eine andere Form der Nichtlinearität bei Material umfasst abrupte Änderungen von Materialeigenschaften, insbesondere der Steifigkeit, die häufig durch Phasenänderungen oder Materialversagen verursacht werden.
2. Nichtlineare Geometrie
Die häufigste Form des Verhaltens nichtlinearer Geometrie ist große Deformation. In diesem Fall ist die Formulierung mit geringer Dehnungsrate, die in der linearen statischen Analyse verwendet wird, nicht mehr gültig. Eine andere Form ist die Starrkörperbewegung, bei der sich der Massenschwerpunkt des Körpers im Laufe der Zeit bewegt oder sich das Objekt um einen Punkt dreht.
3. Nichtlineare Randbedingungen und Lasten
Konvergenz wird in einer impliziten Analyse schwierig, wenn sich eine Last relativ zum Zeitschritt schnell ändert. Dabei kann es sich um eine angewendete Last oder eine Last handeln, die durch Kontakt zwischen zwei Körpern übertragen wird.
Ereignisse mit hoher Geschwindigkeit und kurzer Dauer weisen oft diese Arten von Nichtlinearitäten auf. Die kleinen Zeitschritte, die bei der expliziten Zeitintegration verwendet werden, ermöglichen es, diese Änderungen von einem Schritt zum anderen als linear zu approximieren. Sie ermöglichen es dem Solver auch, interne Kräfte zu berechnen, die nichtlineare Systeme bei Plastizität oder Materialversagen im Gleichgewicht halten.
Annäherung konzentrierter Masse
Ein weiterer Schlüsselaspekt des expliziten Zeitintegrationsansatzes zur Lösung dynamischer Probleme ist die Fähigkeit, die Knotenmasse jedes Elements als konzentrierte Masse darzustellen. Dadurch wird eine Massenmatrix mit einer einzelnen Diagonale erzeugt, sodass die Matrixinvertierung, die zur Berechnung der Trägheitswerte für das Modell erforderlich ist, trivial ist.
Quasistatische Strukturanalyse
Ein Teil der dynamischen Strukturanalyse tritt auf, wenn die Trägheitseffekte in einem System klein genug sind, um ignoriert zu werden, und das System im Wesentlichen die ganze Zeit im Gleichgewicht bleibt. Ein gutes Beispiel für dieses Verhalten ist Metallformung. Sie ist insofern dynamisch, dass die Materialeigenschaften, insbesondere die Plastizität, zeitabhängig sind, aber die Trägheit des Metalls die plastische Deformation nicht beeinflusst.
Was ist implizite Dynamik?
Es ist schwierig, über explizite Dynamik zu sprechen, ohne implizite Dynamik zu diskutieren. Wie der Name schon sagt, ist implizite Dynamik ein FEA-Simulationsansatz, der ein implizites Zeitintegrationsschema verwendet. Wie die explizite Dynamik löst die implizite Dynamik immer noch die vollständige Bewegungsgleichung über die Zeit mit mehreren Zeitschritten.
Die Gleichungen für die implizite Integrationsmethode enthalten Werte für den aktuellen und den nächsten Zeitschritt. Bei Tools für Software für implizite Simulation verwendet der Solver ein Euler-Rückwärts-Verfahren, um Gleichungen für einen Wert im nächsten Zeitschritt abzuleiten, die eine Funktion des aktuellen Schritts (k) und des nächsten Zeitschritts sind:
$$y_{k+1} = \frac{-1 + \sqrt{1 + 4 \Delta t y_k}}{2 \Delta t} $$
Der Unterschied zwischen der impliziten Methode und der expliziten Methode
Techniker*innen verwenden beide Integrationsansätze in der Strukturanalyse für dynamische und quasistatische Simulationen. Wie in der Einleitung erwähnt, besteht der Hauptunterschied darin, dass die Lösung, wenn die PDG in die explizite Methode integriert werden, vollständig durch die resultierende Gleichung bestimmt wird. Bei der impliziten Methode sind die unbekannten Werte implizit, daher muss der Algorithmus lineare Algebra nutzen, um die Lösung zu finden.
Aus realer, praktischer Sicht ergeben sich daraus folgende Unterschiede:
| Implizite Methode | Explizite Methode | |
| Zeitschrittgröße | Vom Benutzenden festgelegt, um Laständerungen zu erfassen und nichtlineare Berechnungen bei der Konvergenz zu unterstützen. Der Zeitschritt ist groß und erfordert sehr wenige Schritte. | Wird durch die Wellenausbreitungsdauer durch das kleinste Element im Netz festgelegt. Die Größe des Zeitschritts liegt im Bereich von Millisekunden, sodass selbst für kurze Dauern viele Schritte erforderlich sind. |
| Zyklen pro Schritt berechnen | Vollständige Lösung gleichzeitiger Gleichungen. Mehrere Lösungen pro Zeitschritt, wenn nichtlineare Berechnungen konvergieren müssen. | Sehr effiziente, explizite Lösung für jeden Schritt mit leicht zu invertierender konzentrierter Masse. |
| Speicheranforderungen | Die Methode impliziter Integration und die vollständige Massenmatrix erfordern deutlich mehr Speicher als explizite Methoden. | Die Methode expliziter Integration und die Formulierung konzentrierter Masse erfordern viel weniger Speicher als implizite Methoden. |
| Konvergenz | Bei jedem Zeitschritt für nichtlineare Berechnungen muss Konvergenz erreicht werden, wodurch ein Gleichgewicht hergestellt wird. | Nicht erforderlich, da ein kleiner Zeitschritt eine lineare Annahme ermöglicht. |
| Gleichgewicht | Erforderlich | Nicht erforderlich |
| Sensitivität der Netzanzahl für Rechenressourcen | Problemabhängig, da die resultierende Matrixbandbreite Lösungszeiten bestimmen. | Linear abhängig von der Anzahl der Elemente. |
| Sensitivität der Elementgröße | Die Laufzeit ist relativ unabhängig von der Größe einzelner Elemente. | Linear abhängig von der Größe des kleinsten Elements. Halbieren des kleinsten Elements verdoppelt die Laufzeit. |
| Kontakt | Muss iteriert werden, bis Kräftegleichgewicht erreicht ist. Die Lösung kann abweichen, wenn abrupte Kontaktänderungen auftreten. | Keine Iteration erforderlich. Bewältigt abrupte Kontaktänderungen gut. |
| Materialversagen | Entfernen der Elementsteifigkeit oder der Verbindung zwischen Elementen kann zu Konvergenzproblemen führen und erfordert oft adaptive Vernetzung. | Reibungslose Handhabung dank des kleinen Zeitschritts. |
| Nichtlinearitäten des Materials | Abrupte Änderungen der Eigenschaften und geringe Steifigkeit können Gleichgewichtsprobleme und somit Konvergenzprobleme verursachen. | Ein kleiner Zeitschritt ermöglicht den linearen Umgang in einem bestimmten Zeitschritt. |
Beispiele für "Explizite Dynamik"-Simulation
Die geringe Größe des Zeitschritts und die in der "Explizite Dynamik"-Analyse verwendete Formulierung konzentrierter Masse machen sie ideal für kurzzeitige Ereignisse mit signifikanten Nichtlinearitäten. Benutzende können diesen Ansatz gegenüber der impliziten Analyse für längere, quasistatische Ereignisse mit Gleichgewichtsproblemen wählen.
Techniker*innen können Lösungen von Ansys für explizite Dynamik wie die Software Ansys LS-DYNA branchenübergreifend nutzen, um schnell nützliche Informationen für hochkomplexe, nichtlineare Struktursimulationen zu generieren. Im Folgenden finden Sie eine Liste mit einigen der häufigeren Anwendungen.
Falltesten
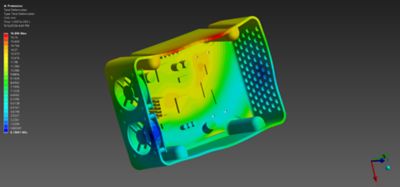
Sowohl Verbraucher- als auch Industrieprodukte müssen während des Versands und Gebrauchs Stürze aus einer angemessenen Höhe überstehen. Daher verwenden Techniker*innen Industrienormen zum Falltesten, um sicherzustellen, dass ihre Produkte ausreichend robust sind. Aber physische Tests sind teuer und erfordern reale Produkte. Die Verwendung eines Tools wie der Software LS-DYNA, das über die Plattform Ansys Workbench mit CAD-Modellen (Computer-Aided Design) verbunden werden kann, reduziert die Kosten und verlagert virtuelle Falltests in einen früheren, kostengünstigeren Teil des Produktentwicklungsprozesses.
Aufprall von Fahrzeugen

Von allen Anwendungen der "Explizite Dynamik"-Simulation hat die Unfallanalyse und -simulation wahrscheinlich die meisten Menschen betroffen und unzählige Leben gerettet. Bei einem Aufprall von Fahrzeugen auf feste Objekte oder andere Fahrzeuge werden Metallstrukturen in einem kurzen Zeitraum gequetscht und versagen – eine ideale Anwendung für explizite Dynamik. Aus diesem Grund simulieren alle Fahrzeughersteller vollständige Fahrzeuge, Sicherheitsgurtsysteme, Airbags und Akkupacks mit einer Anwendung wie der Software LS-DYNA oder ähnlichen Softwaretools.
Aufprall auf menschliche Körper

Ereignisse kurzer Dauer, die Kraft auf ein Objekt übertragen, treten nicht nur bei Produkten und Maschinen auf, sondern wirken auch auf den menschlichen Körper. Aus diesem Grund beziehen Techniker*innen in ihre "Explizite Dynamik"-Simulationen hochgetreue, Strukturmodelle menschlicher Körper wie das Modell Ansys Hans ein. Nicht mehr nur ein Dummy, der Form und Masse darstellt, sondern ein detailliertes menschliches Strukturmodell, das die Lasten und Verletzungsbereiche an jedem Teil der menschlichen Anatomie in einer Vielzahl von Situationen zeigen kann, von Kollisionen von Rennfahrzeugen bis hin zu einem Schlag gegen den Kopf.
Herzsimulation
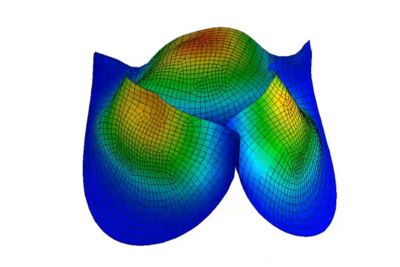
Das menschliche Herz ist eines der komplexesten Beispiele strukturell angetriebener Multiphysik. Elektrische Impulse lösen große Deformationen im Muskelgewebe aus, die wiederum Blut durch sich öffnende und schließende Ventile drücken und saugen. Forscher*innen und Techniker*innen modellieren diese dynamische Interaktion, einschließlich CFD (Computational Fluid Dynamics) von Teilen wie Blutfluss, in einem echten Multiphysik-Tool für explizite Dynamik wie der Software LS-DYNA.
Metallformung
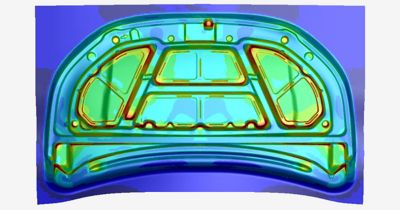
Menschen bringen seit der Bronzezeit Metall in Form, aber im Siliziumzeitalter verwendet man "Explizite Dynamik"-Simulationen, um den Prozess zu optimieren. Die Formungsstufe, in der ein starres Werkzeug dünne Bleche biegt und formt, ist eine ideale Anwendung für die Methode der expliziten Dynamik bei FEA. Im Gegensatz dazu dauern Prozesse wie Rückfederung und Wärmebehandlung länger und lassen sich am besten durch implizite Analysen lösen. Aus diesem Grund können Techniker*innen einen Arbeitsablauf verwenden, der die Simulation entweder im selben Tool von einem expliziten Tool wie der Software LS-DYNA zum impliziten Solver oder zu einer separaten Softwareanwendung wie der strukturellen FEA-Software Ansys Mechanical verschiebt.
Aufschmelzen von Lötmittel
Halbleiterhersteller produzieren jährlich Millionen von Mikrochips, die winzige Lötmittelkugeln verwenden, um Chips physisch und elektrisch zu verbinden. Die Qualität dieser Lötmittelkugeln wirkt sich auf die Leistung, Kühlung und Robustheit fast jedes Elektronikprodukts aus. "Explizite Dynamik"-Simulation kann mit dem stark nichtlinearen Materialverhalten des Lötmittels, wenn es schmilzt, unter Oberflächenspannung fließt und dann erstarrt, umgehen.
Dies sind nur einige der häufigsten Anwendungen von Software-Tools für explizite Dynamik. Weitere Verwendungszwecke sind u. a.:
- Verteidigungsanwendungen, vor allem solche, die Munition und Panzerung betreffen. Die Software Ansys Autodyn ist ein besonders gutes Tool für diese Art von Problemen.
- Bearbeitungsprozesse wie Fräsen und Drehen zur Optimierung von Werkzeugkonstruktion und Bearbeitungsgeschwindigkeit
- Schwappverhalten in Behältern wenn Fahrzeug rangieren
- Beulen von Strukturen unter kritischen Lasten
- Sportartikel, die kurzen, dynamischen Ereignissen ausgesetzt sind
Fortschritte bei der Solver-Funktionalität, den Benutzeroberflächen und der Rechenleistung haben den Einsatz expliziter Dynamik deutlich erweitert. Diese Methode war früher auf High-End-Anwendungen in der Luft- und Raumfahrt und der Verteidigung beschränkt und wird nun bei der Automobilkonstruktion und in vielen anderen Bereichen eingesetzt. Sie ist besonders nützlich in Situationen, in denen kurze, aber intensive Belastungen oder Nichtlinearitäten auftreten, mit denen herkömmliche Solver für implizite Zeitintegration nur schwer umgehen können.
Führende Anbieter wie Ansys bieten außerdem umfangreiche Schulungen, Support und Beispiele an, um Techniker*innen weiterzubilden und ihre Konstruktionen voranzutreiben, um eine höhere Leistung, mehr Sicherheit und verbesserte Haltbarkeit zu erzielen.
Zugehörige Ressourcen
Los geht's
Wenn Sie mit technischen Herausforderungen konfrontiert sind, ist unser Team für Sie da. Mit unserer langjährigen Erfahrung und unserem Engagement für Innovation laden wir Sie ein, sich an uns zu wenden. Lassen Sie uns zusammenarbeiten, um Ihre technischen Hindernisse in Chancen für Wachstum und Erfolg zu verwandeln. Kontaktieren Sie uns noch heute, um das Gespräch zu beginnen.