-
-
Software gratuito per studenti
Ansys potenzia la nuova generazione di ingegneri
Gli studenti hanno accesso gratuito a software di simulazione di livello mondiale.
-
Connettiti subito con Ansys!
Progetta il tuo futuro
Connettiti a Ansys per scoprire come la simulazione può potenziare la tua prossima innovazione.
Paesi e regioni
Customer Center
Supporto
Partner Community
Contatta l'ufficio vendite
Per Stati Uniti e Canada
Accedi
Prove Gratuite
Prodotti & Servizi
Scopri
Chi Siamo
Back
Prodotti & Servizi
Back
Scopri
Ansys potenzia la nuova generazione di ingegneri
Gli studenti hanno accesso gratuito a software di simulazione di livello mondiale.
Back
Chi Siamo
Progetta il tuo futuro
Connettiti a Ansys per scoprire come la simulazione può potenziare la tua prossima innovazione.
Customer Center
Supporto
Partner Community
Contatta l'ufficio vendite
Per Stati Uniti e Canada
Accedi
Prove Gratuite
DETTAGLI DELL'ARGOMENTO
Che cos'è la dinamica esplicita?
Dinamica esplicita è un'espressione che si riferisce ai modelli numerici che rappresentano un comportamento dinamico non lineare, i quali utilizzano il metodo degli elementi finiti (FEM) con un approccio di integrazione temporale esplicita per calcolare la risposta ai carichi applicati in piccoli incrementi di tempo.
L'integrazione temporale esplicita è particolarmente indicata per i problemi non lineari che subiscono un comportamento dipendente dal tempo su brevi periodi. Le applicazioni tipiche per l'analisi dinamica esplicita includono test di caduta, incidenti di veicoli, formatura di metalli e rottura dei materiali.
La simulazione dell'analisi degli elementi finiti (FEA) può anche utilizzare un approccio di integrazione temporale implicito. L'approccio esplicito implica molti piccoli passaggi temporali con calcoli efficienti dal punto di vista computazionale, ma il metodo implicito richiede meno passaggi temporali più rilevanti. Anche i calcoli sono molto più costosi dal punto di vista computazionale. Il metodo migliore è determinato dalla non linearità complessiva del sistema e dalla durata dell'evento.
Metodo degli elementi finiti
Il FEM è un metodo matematico utilizzato per risolvere equazioni differenziali ordinarie o parziali (PDE). Per simulare sistemi fisici, gli utenti suddividono il dominio in blocchi discreti, chiamati elementi finiti, e il software applica a ciascun elemento le equazioni matematiche che descrivono il fenomeno. Lo strumento poi combina le equazioni e vengono utilizzati metodi numerici per risolvere le incognite. L'uso del FEM per modellare sistemi fisici è chiamato analisi degli elementi finiti (FEA).
Non lineare
Nella FEA, il termine "non lineare" indica un comportamento in cui l'equazione che descrive il fenomeno non è lineare. Il comportamento non lineare tipico include modelli di materiali con proprietà non lineari, grandi deformazioni, condizioni di contorno, carichi dinamici, contatti complessi e rottura dei materiali.
Simulazione dinamica
L'equazione completa del movimento per un oggetto è:
Forza = (massa x accelerazione) + (smorzamento x velocità) + (rigidità x deformazione)
Quando l'accelerazione è minima o la velocità è costante, un problema può essere definito statico. In questo scenario, un risolutore FEA deve solo determinare i valori incogniti di forza e deformazione; il tempo non svolge alcun ruolo. Tuttavia, se la velocità cambia, il problema diventa dinamico, perché il fenomeno varia nel corso del tempo.
Metodo di integrazione temporale esplicita
Le equazioni differenziali alle derivate parziali (PDE) in un modello a elementi finiti che rappresenta eventi dinamici vengono risolte a ogni intervallo di tempo. Per questo, il software deve integrarle nel tempo. L'approccio della dinamica esplicita si chiama "esplicito" perché il risultato dell'integrazione fornisce un'equazione che calcola direttamente il valore al passo temporale successivo a partire dai valori noti al passo attuale. L'altro metodo utilizzato nell'analisi agli elementi finiti, l'integrazione temporale implicita, si chiama "implicito" perché il valore desiderato al passo successivo viene determinato solo indirettamente tramite un'equazione che coinvolge sia valori noti sia incogniti. In questo caso, il risolutore usa l'algebra lineare per calcolare le incognite implicite.
Un esempio del metodo esplicito è il metodo di Eulero in avanti che porta a un'equazione che dipende solo dal passo temporale corrente:
$$y_{k+1} = y_k - \Delta t \, y_k^2 $$
Aspetti principali dell'analisi dinamica esplicita
Quando si utilizza il metodo di soluzione dinamica esplicita nei software di simulazione, sia i principianti sia gli ingegneri esperti devono essere consapevoli di alcuni aspetti importanti della metodologia, determinati dagli algoritmi matematici utilizzati.
Passo temporale critico e tempo di propagazione dell'onda
L'informazione più importante da considerare è che la soluzione esplicita calcola i valori al passo temporale immediatamente successivo a quello corrente. Poiché il risolutore determina come varia la deformazione durante il passo temporale, la dimensione del passo è limitata al tempo necessario a un'onda di deformazione per attraversare l'elemento più piccolo del modello. Questo limite è chiamato passo temporale critico, e la velocità con cui il suono si propaga nel materiale determina il tempo di propagazione dell'onda. Per materiali rigidi e per elementi di piccole dimensioni, il passo temporale critico è generalmente dell'ordine dei millisecondi.
Comportamento non lineare
Un altro aspetto che gli ingegneri devono conoscere riguarda i diversi tipi di comportamento non lineare che la dinamica esplicita può catturare. Poiché l'approccio esplicito utilizza passi temporali molto piccoli, è in grado di trattare il cambiamento in un valore calcolato su quel breve intervallo come lineare.
Gli ingegneri classificano la maggior parte dei comportamenti non lineari di una simulazione FEA in una delle seguenti categorie:
1. Materiali non lineari
I materiali non lineari hanno proprietà che cambiano in modo non lineare a causa dei carichi applicati o del tempo. La forma più comune di non linearità dei materiali, presente quasi in ogni tipo di analisi, è la plasticità. L'approccio implicito può incontrare difficoltà nel determinare la convergenza per alti livelli di plasticità, soprattutto quando la rigidità del materiale diminuisce. Strettamente legate alla plasticità sono le proprietà dipendenti dalla velocità di deformazione, come la rigidità. Un'altra forma di non linearità dei materiali riguarda cambiamenti improvvisi delle proprietà del materiale, in particolare della rigidità, spesso causati da cambiamenti di fase o da rottura del materiale.
2. Geometria non lineare
La forma più comune di non linearità geometrica è la grande deformazione. In questo caso, la formulazione a piccole deformazioni utilizzata nelle analisi statiche lineari non è più valida. Un'altra forma è il moto di corpo rigido, in cui il centro di massa del corpo si sposta nel tempo oppure l'oggetto ruota attorno a un punto.
3. Condizioni di contorno e carichi non lineari
Nelle analisi implicite, la convergenza diventa difficile quando un carico cambia rapidamente rispetto alla durata del passo temporale. Questo può riguardare un carico applicato o un carico trasmesso attraverso il contatto tra due corpi.
Eventi ad alta velocità e di breve durata spesso presentano questi tipi di non linearità. I piccoli passi temporali utilizzati nell'integrazione temporale esplicita permettono di approssimare questi cambiamenti come lineari da un passo all'altro. Consentono inoltre al risolutore di calcolare le forze interne necessarie a mantenere l'equilibrio durante fenomeni di plasticità o rottura dei materiali.
Approssimazione della massa concentrata
Un altro aspetto chiave dell'integrazione temporale esplicita per la risoluzione di problemi dinamici è la possibilità di rappresentare la massa nodale di ciascun elemento come massa concentrata. Questo produce una matrice di massa diagonale, quindi l'inversione della matrice necessaria per calcolare i valori inerziali del modello diventa molto semplice.
Analisi strutturale quasi-statica
Un sottoinsieme dell'analisi strutturale dinamica si verifica quando gli effetti inerziali di un sistema sono così ridotti da poter essere trascurati, e il sistema rimane sostanzialmente in equilibrio per tutto il tempo. Un buon esempio di questo tipo di comportamento è la formatura dei metalli. Si tratta di un fenomeno dinamico perché le proprietà del materiale, in particolare la plasticità, dipendono dal tempo, ma l'inerzia del metallo non influisce sulla sua deformazione plastica.
Che cos'è la dinamica implicita?
È difficile parlare di dinamiche esplicite senza considerare anche le dinamiche implicite. Come suggerisce il nome, la dinamica implicita è un approccio di simulazione FEA che utilizza uno schema di integrazione del tempo implicito. Come la dinamica esplicita, la dinamica implicita risolve ancora l'equazione completa del movimento nel tempo con più passi temporali.
Le equazioni per il metodo di integrazione implicita coinvolgono valori sia per il passo temporale corrente che per quello successivo. Nei software di simulazione impliciti, il risolutore utilizza il metodo di Eulero all'indietro per ricavare equazioni che calcolano un valore al passo temporale successivo come funzione del passo corrente (k) e di quello successivo:
$$y_{k+1} = \frac{-1 + \sqrt{1 + 4 \Delta t y_k}}{2 \Delta t} $$
La differenza tra il metodo implicito e i metodi espliciti
Gli ingegneri utilizzano entrambi gli approcci di integrazione nell'analisi strutturale per simulazioni dinamiche e quasi statiche. Come accennato nell'introduzione, la differenza principale è che, quando le equazioni differenziali alle derivate parziali (PDE) vengono integrate con il metodo esplicito, la soluzione è completamente definita dall'equazione risultante. Nel metodo implicito, invece, i valori incogniti sono impliciti, quindi l'algoritmo deve utilizzare l'algebra lineare per trovare la soluzione.
Dal punto di vista pratico, ciò comporta le seguenti differenze:
| Metodo implicito | Metodo esplicito | |
| Dimensione del passo temporale | Impostato dall'utente per acquisire le variazioni di carico e favorire la convergenza nei calcoli non lineari. Il passo temporale è ampio e richiede pochi passaggi. | Impostato in base al tempo di propagazione dell'onda attraverso l'elemento più piccolo nella mesh. Il passo temporale è nell'ordine di millisecondi e richiede molti passaggi anche per brevi durate. |
| Cicli di calcolo per passo | Soluzione completa di equazioni simultanee. Più soluzioni per ciascun passo temporale se necessario per la convergenza dei calcoli non lineari. | Soluzione esplicita molto efficiente per ciascun passo, con massa concentrata facilmente invertibile. |
| Requisiti di memoria | Il metodo di integrazione implicita e la matrice di massa completa richiedono una quantità di memoria significativamente maggiore rispetto ai metodi espliciti. | Il metodo di integrazione esplicita e la formulazione con massa concentrata richiedono una quantità di memoria molto inferiore rispetto ai metodi impliciti. |
| Convergenza | Necessaria in ogni passo temporale per i calcoli non lineari, per garantire l'equilibrio. | Non necessaria, perché un passo temporale ridotto consente di assumere linearità. |
| Equilibrio | Necessario | Non necessario |
| Sensibilità della mesh rispetto alle risorse di calcolo | Dipende dal problema, perché la larghezza di banda della matrice risultante influisce sui tempi di risoluzione. | Dipende in modo lineare dal numero di elementi. |
| Sensibilità delle dimensioni degli elementi | Il tempo di calcolo è relativamente indipendente dalle dimensioni dei singoli elementi. | Dipende in modo lineare dalla dimensione dell'elemento più piccolo. Dimezzando l'elemento più piccolo, il tempo di calcolo si raddoppia. |
| Contatti | È necessario ripetere fino al raggiungimento dell'equilibrio delle forze. La soluzione può divergere se i contatti variano bruscamente. | Non è richiesta alcuna iterazione. Gestisce in modo efficace i cambiamenti bruschi dei contatti. |
| Rottura materiale | La rimozione della rigidità degli elementi o della connessione tra gli elementi può causare problemi di convergenza e spesso richiede il meshing adattivo. | Gestito in modo fluido grazie a un passo temporale ridotto. |
| Non linearità del materiale | Cambiamenti bruschi nelle proprietà e bassa rigidità possono provocare problemi di equilibrio e, quindi, difficoltà di convergenza. | Un passo temporale ridotto consente di trattare il fenomeno come lineare in ciascun intervallo di tempo. |
Esempi di simulazione dinamica esplicita
Le dimensioni ridotte del passo temporale e la formulazione con massa concentrata utilizzati nell'analisi dinamica esplicita rendono questo approccio ideale per eventi di breve durata con significative non linearità. Gli utenti possono scegliere questo approccio rispetto all'analisi implicita anche per eventi più lunghi e quasi statici in cui si presentano problemi di equilibrio.
Gli ingegneri possono utilizzare le soluzioni di dinamica esplicita di Ansys, come il software Ansys LS-DYNA, in diversi settori per ottenere rapidamente informazioni utili per simulazioni strutturali altamente complesse e non lineari. Di seguito è riportato un elenco di alcune delle applicazioni più comuni.
Test di caduta
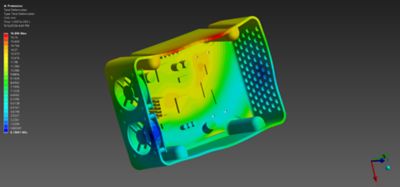
Sia i prodotti di consumo sia quelli industriali devono resistere a cadute da un'altezza ragionevole durante la spedizione e l'uso; per questo gli ingegneri utilizzano standard industriali per i test di caduta al fine di garantire che i prodotti siano sufficientemente robusti. Tuttavia, l'esecuzione di test fisici è costosa e richiede hardware reali. L'uso di uno strumento come il software LS-DYNA, che può collegarsi ai modelli di progettazione assistita da computer (CAD) tramite la piattaforma Ansys Workbench riduce i costi e consente di effettuare test di caduta virtuali in una fase iniziale e meno costosa del processo di sviluppo del prodotto.
Impatto dei veicoli

Tra tutte le applicazioni della simulazione dinamica esplicita, l'analisi e la simulazione degli incidenti automobilistici sono probabilmente quelle che hanno coinvolto il maggior numero di persone e salvato innumerevoli vite. L'impatto di un veicolo contro un oggetto solido o un altro veicolo comporta la deformazione e la rottura delle strutture metalliche in un breve intervallo di tempo, rendendo questa situazione un'applicazione ideale per la dinamica esplicita. Ecco perché tutti i produttori di veicoli simulano veicoli interi, sistemi delle cinture di sicurezza, airbag e gruppi batterie utilizzando un'applicazione come il software LS-DYNA o strumenti simili.
Impatto sul corpo umano

Gli eventi di breve durata che trasmettono forza a un oggetto non riguardano solo prodotti e macchinari, ma influenzano anche il corpo umano. Per questo motivo, gli ingegneri includono nei loro modelli di simulazione dinamica esplicita modelli strutturali ad alta fedeltà del corpo umano, come il modello Ansys Hans nelle loro simulazioni dinamiche esplicite. Non si tratta più solo di un semplice manichino che rappresenta forma e massa, bensì di un modello strutturale umano dettagliato che può mostrare le sollecitazioni e le aree di possibile lesione in qualsiasi parte dell’anatomia umana in diverse situazioni, dagli incidenti con auto da corsa alle collisioni con un pugno alla testa.
Simulazione cardiaca
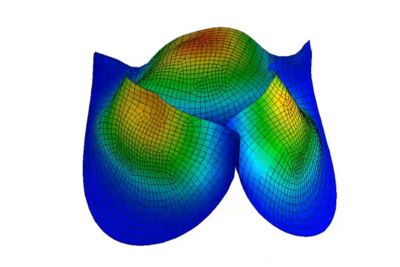
Il cuore umano è uno degli esempi più complessi di fenomeni multifisici guidati dalla struttura. Gli impulsi elettrici innescano grandi deformazioni nei tessuti muscolari, che a loro volta spingono e tirano il sangue attraverso le valvole che si aprono e si chiudono. Ricercatori e ingegneri modellano questa interazione dinamica, includendo la fluidodinamica computazionale (CFD) di elementi come il flusso sanguigno, utilizzando un vero strumento di dinamica esplicita multifisica come il software LS-DYNA.
Formatura di metalli
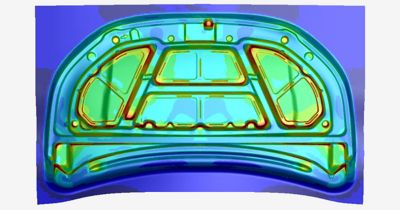
Gli esseri umani hanno dato forma al metallo fin dall'era del bronzo, ma nell'era del silicio utilizziamo la simulazione dinamica esplicita per ottimizzare il processo. La fase di formatura, in cui uno strumento rigido si piega e forma lamiere sottili, è un'applicazione ideale per il metodo dinamico esplicito in FEA. Al contrario, i processi come la springback e il trattamento termico hanno una durata maggiore e vengono risolti meglio tramite l'analisi implicita. Per questo motivo, gli ingegneri possono utilizzare un flusso di lavoro che sposta la simulazione da uno strumento esplicito come il software LS-DYNA al risolutore implicito nello stesso strumento o a un'applicazione software separata come il software FEA strutturale Ansys Mechanical.
Saldatura a riflusso
I produttori di semiconduttori producono ogni anno milioni di microchip che utilizzano piccole sfere di saldatura per collegare fisicamente ed elettricamente i chip. La qualità di queste sfere di saldatura influisce sulle prestazioni, sul raffreddamento e sulla robustezza di quasi tutti i prodotti elettronici. La simulazione dinamica esplicita è in grado di gestire il comportamento altamente non lineare dei materiali della saldatura durante la fusione, il flusso sotto tensione superficiale e la solidificazione.
Queste sono solo alcune delle applicazioni più comuni degli strumenti software dinamici espliciti. Altri usi includono:
- applicazioni per la difesa, in particolare quelle che coinvolgono munizioni e armature. Il software Ansys Autodyn è uno strumento particolarmente adatto per questa classe di problemi.
- Processi di lavorazione come fresatura e tornitura per ottimizzare il design degli utensili e la velocità di lavorazione
- Comportamento in pendenza nei container durante le manovre del veicolo
- Cedimento delle strutture sotto carichi critici
- Prodotti sportivi soggetti a eventi brevi e dinamici
I progressi nella funzionalità dei risolutori, nelle interfacce utente e nella potenza di elaborazione hanno ampliato notevolmente l'uso della dinamica esplicita. Una volta limitato alle applicazioni high-end del settore aerospaziale e difesa, questo metodo viene ora utilizzato nella progettazione automobilistica e in molti altri campi. È particolarmente utile in situazioni che comportano carichi brevi ma intensi o non linearità che i risolutori di integrazione del tempo impliciti tradizionali faticano a gestire.
Fornitori leader come Ansys provvedono inoltre a offrireformazione, supporto ed esempi avanzati per aiutare gli ingegneri a diventare esperti e a guidare i progetti per ottenere prestazioni migliori, maggiore sicurezza e maggiore durata.
Risorse correlate
Cominciamo
Se devi affrontare sfide di progettazione, il nostro team è a tua disposizione per assisterti. Con una vasta esperienza e un impegno per l'innovazione, ti invitiamo a contattarci. Collaboriamo per trasformare i tuoi ostacoli ingegneristici in opportunità di crescita e successo. Contattaci oggi stesso per iniziare la conversazione.