什么是显式动力学?
显式动力学是指用于表示非线性动力学行为的数值模型,这些模型使用有限元法(FEM)和显式时间积分法,将时间划分为非常小的增量,来逐步计算对外加载荷作用下的响应。
显式时间积分最适合用于非线性、在较短时间内发生随时间变化行为的问题。显式动力学分析的典型应用包括跌落测试、车辆碰撞、金属成形和材料失效。
有限元分析(FEA)仿真还可以使用隐式时间积分法。显式方法把时间切分成非常多的小时间步,每一步的计算效率高;而隐式方法则是使用较少但更大的时间步,其计算成本也明显更高。要确定哪种方法是最佳的,取决于系统的整体非线性和事件的持续时间。
有限元法
FEM是一种用于求解常微分方程或偏微分方程(PDE)的数学方法。对物理系统进行仿真时,用户会将整体区域划分成离散的小单元(称为有限元),然后仿真软件对每个单元分别应用PDE进行求解。然后,软件工具会组合这些单元方程,并使用数值求解器来求解未知量。这种使用FEM对物理系统进行建模的过程,被称为有限元分析(FEA)。
非线性
在FEA中,“非线性”是指,其代表性方程不是线性方程的行为。典型的非线性行为包括非线性材料模型、大变形、边界条件、动态载荷、复杂接触和材料失效。
动力学仿真
表示物体运动的完整方程为:
力=(质量x加速度)+(阻尼x速度)+(刚度x位移)
当最小加速度或速度恒定时,则称为静态问题。在这种场景中,FEA求解器只需确定力和位移的未知值;该情况下不涉及时间因素。如果速度有变化,该问题则称为动态问题,因为其随时间变化而变化。
显式时间积分法
在有限元模型中,表示动态事件的PDE会在给定的时间步下进行求解。因此,软件必须对PDE进行时间积分运算。我们将显式动力学方法称为“显式(explicit)”,原因在于积分的结果是一个方程,该方程可以针对当前时间步的已知量,直接计算下一个时间步的值。FEA中使用的另一种方法是隐式时间积分,之所以被称为“隐式(implicit)”,是因为下一个时间步的目标值不是直接计算,而是通过包含已知量和未知量的方程进行间接确定。在这种情况下,求解器使用线性代数来计算隐含的未知值。
显式方法的一个示例为前向欧拉法(Forward Euler Method),其得到的方程仅与当前时间步有关:
$$y_{k+1} = y_k - \Delta t \, y_k^2 $$
显式动力学分析的重要方面
在仿真软件中使用显式动力学求解方法时,无论是仿真初学者,还是经验丰富的工程师,都需要了解这种方法中由数学算法决定的一些重要方面。
临界时间步长和波传播时间
最重要的一点是,显式求解每次只求解“当前时间步之后的时间步”。显式求解器是在每个时间步内计算应变是如何变化的,因此时间步长必须小于应变波穿过模型中最小单元所需的时间。这一限制被称为临界时间步长,而声音穿过材料的速度决定了波传播时间。对于刚度大的材料和小单元尺寸,关键时间步通常约为毫秒级。
非线性行为
工程师还需要关注的是,显式动力学可以捕获哪些类型的非线性行为。由于显式方法采用的时间步非常小,因此求解器可以将计算得到的值在该小时间步上的变化视为线性的。
工程师将FEA仿真中的大多数非线性行为分为以下类别之一:
1.非线性材料
非线性材料的属性会根据载荷或时间,以非线性方式发生变化。在几乎任何分析类型中,最常见的材料非线性形式都是塑性。隐式方法可能难以确定更高塑性水平的收敛,尤其是当材料刚度下降时。与塑性密切相关的是应变速率相关的属性,如刚度。另一种材料非线性形式涉及材料属性(尤其是刚度)的突变,这通常是由相变或材料失效引起的。
2.非线性几何结构
非线性几何结构行为最常见的形式是大变形。在这种情况下,线性静态分析中使用的小应变率公式不再有效。另一种形式是刚体运动,在这种情况下,几何体的质心随着时间而移动,或者物体围绕一个点旋转。
3.非线性边界条件和载荷
在隐式分析中,当载荷相对于时间步快速变化时,很难实现收敛。其中,载荷可以是通过两个几何体之间的接触而施加的或传递的。
高速、短时间事件通常表现出这类非线性。显式时间积分中使用的时间步较小,因此一个时间步到另一个时间步的这些变化,能够近似为线性变化。同时,其还使求解器能够计算在发生塑性或材料失效时,使非线性系统保持平衡所需的内部力。
集中质量近似
在求解动力学问题时,显式时间积分法的另一个关键方面是,它能够将每个单元的节点质量表示为集中质量。这样,就会生成一个仅包含单个对角线的质量矩阵,因此计算模型惯性值所需的矩阵求逆将非常简单。
准静态结构分析
在某些动态结构分析中,如果系统中的惯性效应小到足以被忽略的程度,系统在整个过程中实际上始终处于平衡状态。金属成形就是上述情况的一个良好示例——其之所以是动态问题,原因在于材料属性(尤其是塑性)与时间相关,但金属的惯性不会影响其塑性变形。
什么是隐式动力学?
在讨论显式动力学时,很难不提及隐式动力学。顾名思义,隐式动力学是一种使用隐式时间积分法的FEA仿真方法。与显式动力学一样,隐式动力学仍然利用多个时间步来求解运动随时间变化的完整方程。
隐式积分法的方程,涉及当前时间步和下一个时间步的值。对于隐式仿真软件工具,求解器使用后向欧拉法(Backward Euler Method)推导方程,以求得下一个时间步的值,该方程与当前步长(k)和下一个时间步有关:
$$y_{k+1} = \frac{-1 + \sqrt{1 + 4 \Delta t y_k}}{2 \Delta t} $$
隐式方法和显式方法之间的区别
在结构分析中,工程师使用这两种积分方法进行动态和准静态仿真。如上所述,两者的主要区别在于,当在显式方法中进行PDE积分运算时,解完全由得到的方程来确定;在隐式方法中,未知值是隐含的,因此算法必须使用线性代数来找到解。
从现实世界的实际角度来看,这会带来以下差异:
| 隐式方法 | 显式方法 | |
| 时间步长 | 由用户设置,以捕获载荷中的变化,并帮助非线性计算实现收敛。时间步很大,只需很少的步数。 | 由波穿过网格中最小单元的传播时间定义。时间步长约为毫秒级,即使对于短时间事件也需要许多步。 |
| 每步计算周期 | 完整求解联立方程。如果非线性计算需要收敛,每个时间步需要多次求解。 | 每个时间步都采用非常高效的显式求解,且采用了集中质量,易于求逆。 |
| 内存要求 | 与显式方法相比,隐式积分法和全质量矩阵需要的内存更多。 | 与隐式方法相比,显式积分法和集中质量公式需要的内存更少。 |
| 收敛 | 非线性计算的每个时间步都必须实现收敛,以建立平衡。 | 不需要收敛,因为较小的时间步允许线性假设。 |
| 平衡 | 需要 | 不需要 |
| 网格数量对计算资源的敏感性 | 与问题相关,因为得到的矩阵带宽将决定求解时间。 | 与单元数量线性相关。 |
| 单元尺寸敏感度 | 运行时间与单个单元的尺寸相对独立。 | 与最小单元尺寸线性相关。当最小单元尺寸缩小一半时,运行时间就会增加一倍。 |
| 接触 | 必须迭代,直到达到力平衡。当接触发生突然变化时,求解可能会发散。 | 无需迭代。能够很好地处理接触的突然变化。 |
| 材料失效 | 去除单元刚度或单元之间的连接,可能会导致收敛问题,并且通常需要自适应网格划分。 | 由于时间步较小,因此能够流畅地处理。 |
| 材料非线性 | 材料属性的突然变化和低刚度会导致平衡问题,从而引发收敛问题。 | 时间步足够小时,可以在该时间步内将问题按线性方式处理。 |
显式动力学仿真示例
显式动力学分析中使用的小时间步长和集中质量公式,使其非常适合用于分析持续时间短但具有显著非线性的事件。用户也可能会选择这种方法,而非隐式分析,来处理持续时间较长但存在平衡问题的准静态事件。
工程师可以在各个行业中使用Ansys LS-DYNA软件等Ansys显式动力学解决方案,为高度复杂的非线性结构仿真快速生成有用的信息。下面列出了一些较为常见的应用。
跌落测试
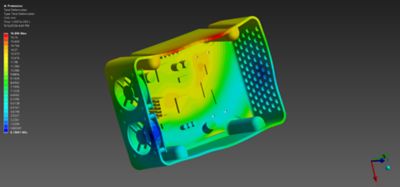
消费类产品和工业品都需要在运输和使用过程中承受从合理高度跌落的情况,因此工程师基于行业标准进行跌落测试,以确保其产品足够稳健可靠。但是,开展物理测试的成本高昂,而且需要依赖实际的硬件设备。利用像LS-DYNA软件这样的工具,并通过Ansys Workbench平台连接到计算机辅助设计(CAD)模型,可以降低成本,并将虚拟跌落测试提前到产品开发流程中更早、成本更低的阶段。
车辆碰撞


这类在极短时间内向物体施加力的事件,不仅会发生在产品和机械系统上,而且还会作用于人体。因此,工程师在显式动力学仿真中纳入了高保真度、结构化的人体模型,如Ansys Hans模型。这是一种详细的人体结构模型,而不再只是一个表示形状和重量的假人,它可以在从赛车碰撞到头部冲击等各种情况下,显示人体结构任何部位的载荷和受伤区域。
心脏仿真
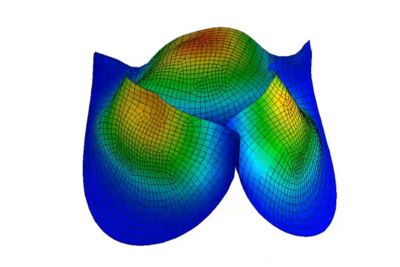
人体心脏,是结构驱动型多物理场系统中最复杂的案例之一。电脉冲会触发肌肉组织中的大变形,进而推动和拉动血液,使其通过周期性开合的瓣膜。研究人员和工程师使用多物理场显式动力学工具(如LS-DYNA软件)对这种动态相互作用进行建模,其中包括血流等部位的计算流体力学(CFD)。
金属成形
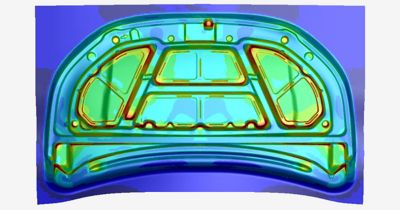
自青铜器时代以来,人类一直在将金属锻造成不同形状,但在硅时代,我们使用显式动力学仿真来优化工艺。在金属成形阶段,刚性工具将金属弯曲、使金属薄板成形,这是FEA显式动力学方法的理想应用领域。反之,对于回弹和热处理等持续时间更长的工艺,最好通过隐式分析来求解。因此,工程师可以使用工作流程,将仿真从显式工具(如LS-DYNA软件)传输到该工具的隐式求解器,或传输到不同的软件应用(如Ansys Mechanical结构FEA软件)。
回流焊接
半导体制造商每年生产数百万颗微芯片,这些微芯片通过微小的焊球实现物理和电气连接。焊球的质量会影响几乎所有电子产品的性能、散热和稳健性。显式动力学仿真可以处理焊料熔化、在表面张力下流动然后固化时的高度非线性材料行为。
上述只是显式动力学软件工具的几个常见应用,其他应用领域包括:
- 国防应用,尤其是涉及弹药和装甲的应用。Ansys Autodyn软件是解决这类问题的出色工具。
- 铣削和车削等加工工艺,以优化刀具设计和加工速度
- 在车辆行驶时,箱体中的晃动行为
- 结构在临界载荷下的屈曲
- 承受短时间动态载荷的体育器材产品
求解器功能、用户界面和计算能力的发展进步,大幅拓展了显式动力学的应用范围。这种方法曾经仅限于高端航空航天和国防(A&D)应用,现在已广泛应用于汽车设计和许多其他领域。在传统隐式时间积分求解器难以处理的短时间、剧烈载荷情况或非线性情况中,该方法尤其有价值。
Ansys等业界领先的供应商还提供广泛的培训、支持和示例,以帮助工程师熟练掌握并推动产品设计,从而提高性能、安全性和耐久性。
相关资源
现在就开始行动吧!
如果您面临工程方面的挑战,我们的团队将随时为您提供帮助。我们拥有丰富的经验并秉持创新承诺,期待与您联系。让我们携手合作,将您的工程挑战转化为价值增长和成功的机遇。欢迎立即联系我们进行交流。