-
-
Accédez au logiciel étudiant gratuit
Ansys donne les moyens à la prochaine génération d'ingénieurs
Les étudiants ont accès gratuitement à un logiciel de simulation de classe mondiale.
-
Connectez-vous avec Ansys maintenant !
Concevez votre avenir
Connectez-vous à Ansys pour découvrir comment la simulation peut alimenter votre prochaine percée.
Pays et régions
Espace client
Support
Communautés partenaires
Contacter le service commercial
Pour les États-Unis et le Canada
S'inscrire
Essais gratuits
Produits & Services
Apprendre
À propos d'Ansys
Back
Produits & Services
Back
Apprendre
Ansys donne les moyens à la prochaine génération d'ingénieurs
Les étudiants ont accès gratuitement à un logiciel de simulation de classe mondiale.
Back
À propos d'Ansys
Concevez votre avenir
Connectez-vous à Ansys pour découvrir comment la simulation peut alimenter votre prochaine percée.
Espace client
Support
Communautés partenaires
Contacter le service commercial
Pour les États-Unis et le Canada
S'inscrire
Essais gratuits
INFORMATIONS SUR LE SUJET
Qu'est-ce que l'optimisation de la topologie ?
L'optimisation topologique (TO ou TopOpt) est une méthodologie permettant de déterminer la conception optimale d'un objet pour atteindre un objectif spécifique, compte tenu d'un ensemble de contraintes, de charges et de conditions limites, en ajoutant ou en supprimant des fonctionnalités géométriques et en ajustant leur taille.
Contrairement à l'optimisation de forme traditionnelle, qui ne modifie que la taille d'une topologie prédéfinie, l'optimisation topologique utilise des algorithmes pour ajouter et supprimer des matériaux dans un espace de conception spécifié afin d'atteindre des objectifs de performance. Il s'agit notamment de limiter la masse, de maintenir une plage de température, d'éviter certaines fréquences de résonance ou de maintenir les contraintes et les déformations dans les limites autorisées. En utilisant la méthode d'optimisation topologique, les ingénieurs laissent les performances d'un objet déterminer la disposition optimale des matériaux.
L'optimisation topologique était initialement limitée à la recherche et au développement (R&D), car les géométries obtenues ne pouvaient pas être fabriquées à l'aide des méthodes de fabrication traditionnelles. Cependant, la fabrication additive, en particulier l'impression 3D de métaux, permet aux concepteurs de produire les formes naturelles générées par l'optimisation topologique. L'introduction de contraintes de fabrication dans les outils d'optimisation topologique permet de contrôler la géométrie afin que les entreprises puissent fabriquer leurs produits à l'aide de techniques de fabrication standard telles que le moulage et le formage.
Deux autres avancées techniques ont permis à un plus grand nombre d'entreprises d'intégrer l'optimisation topologique dans leur processus de conception.
La première a consisté à coupler les algorithmes d'optimisation topologique avec des outils de simulation multiphysique tels que le logiciel Ansys Mechanical ou le logiciel Ansys LS-DYNA. Cela a permis aux ingénieurs d'aller au-delà de la simple optimisation structurelle et d'inclure la chaleur, l'acoustique, le flux de fluide et même l'électromagnétisme dans leur optimisation.
La possibilité de convertir facilement la topologie obtenue en un modèle volumique valide constitue la deuxième avancée. Auparavant, la méthode d'optimisation topologique créait une représentation à facettes qui obligeait les utilisateurs experts à créer un modèle valide dans un logiciel de conception assistée par ordinateur (CAD) en utilisant le résultat de l'optimisation topologique pour se guider. Des outils plus récents, comme le logiciel Ansys Discovery, ajustent et lissent automatiquement la surface optimisée une fois que les itérations ont convergé vers une conception finale.
Combinées à un nombre croissant de formulations d'optimisation et à une vitesse de calcul de plus en plus élevée, ces améliorations ont porté l'optimisation topologique au cœur de la conception de produits.
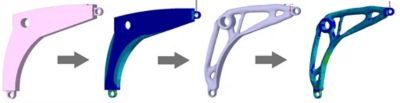
Étapes de l'optimisation topologique utilisées pour réduire le poids d'un levier coudé. De gauche à droite : la géométrie d'origine, le profil de contrainte de la géométrie d'origine, la géométrie à la topologie optimisée et le profil de contrainte de la géométrie à la topologie optimisée.
Fonctionnement de l'optimisation topologique
La meilleure façon de visualiser l'optimisation topologique est d'examiner la forme la plus simple de l'optimisation de la topologie, l'optimisation structurelle binaire. Imaginez une masse volumique remplissant l'espace de conception à optimiser. L'ingénieur crée un modèle FEA représentant la géométrie volumique initiale, puis définit la manière dont l'objet est maintenu, les forces appliquées, les propriétés des matériaux qu'il contient et la contrainte maximale autorisée. Le logiciel FEA discrétise ensuite l'espace de conception et résout les valeurs inconnues.
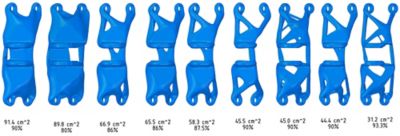
Exemple d'étapes multiples dans l'optimisation topologique structurelle d'un support
Une fois que le modèle résout le défi et produit un résultat, l'algorithme d'optimisation d'un outil d'optimisation topologique évalue chaque élément du modèle FEA pour déterminer s'il est soumis à des charges. Si ce n'est pas le cas pour un élément, l'algorithme le supprime. La rigidité et la densité de chaque élément sont traitées comme des variables binaires, car les propriétés mécaniques de l'élément peuvent soit contribuer pleinement à la rigidité et à la masse de la structure, soit ne pas y contribuer du tout. Cette approche simplifie et accélère le processus d'optimisation en activant ou en désactivant simplement les éléments plutôt qu'en calculant une valeur intermédiaire.
Ce processus se répète au cours des itérations suivantes jusqu'à ce que la masse minimale soit atteinte tout en maintenant la contrainte maximale en dessous de la valeur autorisée. Le modèle obtenu est grossier et épais, similaire à un modèle Lego. Pour le rendre fabricable, l'ingénieur utilise la forme obtenue en tant que guide pour créer un modèle CAD affiné. Ce processus peut être simplifié grâce à des fonctionnalités telles qu'AutoSkin et SubD dans le logiciel Discovery. Ce modèle final est utilisé pour créer un modèle FEA de vérification afin de garantir que la distribution finale des matériaux répond aux exigences de conception.
Toute optimisation topologique est une variante de cette approche d'analyse structurelle de base, avec une complexité accrue au niveau des charges, de la physique et des objectifs.
6 variantes de l'optimisation topologique
Les variantes suivantes augmentent l'étendue des applications et améliorent la précision de la géométrie obtenue.
1. Variables continues
Dans sa forme la plus simple, la méthode d'optimisation topologique consiste à ajouter ou à supprimer des éléments dans le domaine de conception. Lorsque la discrétisation est assez grossière, la topologie obtenue peut se présenter sous forme de blocs et être difficile à convertir en surfaces lisses. Les variables binaires introduisent également une instabilité numérique dans la simulation. Pour résoudre ces problèmes, des techniques d'optimisation topologiquee plus avancées utilisent des variables continues pour des caractéristiques telles que la rigidité, la conductivité thermique ou la densité.
2. Fonctions objectives multivariables
Les algorithmes d'optimisation topologique modifient de manière itérative les variables de l'espace de conception pour atteindre un objectif, appelé fonction objective. Dans de nombreux cas, il n'y a qu'une seule fonction objective : la masse. Cependant, dans le monde réel, l'ingénierie implique généralement plusieurs objectifs, souvent contradictoires. Les logiciels avancés d'optimisation topologique peuvent gérer simultanément plusieurs objectifs en utilisant des fonctions objectives multivariables et des méthodes mathématiques plus complexes.
3. Multiphysique
La plupart des outils d'optimisation de la conception ne concernent qu'un seul domaine physique, généralement structurel. Cependant, étant donné que la méthode des éléments finis (FEM) prend en charge plusieurs domaines physiques, des outils logiciels plus avancés utilisent un processus d'optimisation capable de trouver des solutions optimales pour plusieurs types de charges et de résultats. Les logiciels courants d'optimisation topologique multiphysique combinent la structure, la dynamique structurelle, le transfert de chaleur et le flux de fluide en un seul problème d'optimisation.
4. Paramètres de conception
Les utilisateurs peuvent également orienter leurs conceptions vers des solutions plus pratiques en définissant des paramètres de conception qui peuvent varier dans une plage donnée. Ces paramètres peuvent être aussi simples qu'une liste de tailles de trous standard ou une plage de rayons d'angle, ou aussi complexes que des propriétés de matériaux non linéaires, un espacement minimal entre les fonctionnalités ou des moments d'inertie.
5. Contraintes de fabrication
L'inclusion de contraintes de fabrication est l'une des avancées les plus importantes des outils d'optimisation topologique. Il peut s'agir de contraintes liées au processus de fabrication additive utilisé pour construire la pièce. Pour le fraisage traditionnel, les contraintes peuvent inclure des rayons minimaux, une profondeur maximale ou l'élimination des surplombs. Pour les pièces moulées, des caractéristiques telles que l'épaisseur de paroi minimale, les angles de dépouille et les surplombs sont souvent spécifiées.
6. Variations des propriétés des matériaux
La variation des propriétés des matériaux est un domaine lié à l'optimisation topologique, mais distinct de celle-ci. Les utilisateurs peuvent spécifier une plage de variables continues ou une liste de variables discrètes que l'algorithme d'optimisation doit prendre en compte dans son algorithme d'optimisation.
Les avantages de l'optimisation topologique
L'optimisation topologique est devenue un outil de conception puissant, car elle libère les ingénieurs des limites d'une forme prédéfinie. Au lieu de partir d'une géométrie hypothétique et de la modifier pour répondre aux exigences de conception, l'optimisation de la topologie ajoute et supprime des fonctionnalités en fonction des charges auxquelles l'objet est soumis. Cette approche apporte des améliorations spécifiques et mesurables :
- Réduction du poids : Le principal avantage de l'optimisation topologique est de retirer autant de matériau que possible tout en préservant l'intégrité structurelle. Cela permet de réduire à la fois la masse et la quantité de matériau utilisé.
- Amélioration des performances : Les algorithmes d'optimisation topologique façonnent la topologie pour atteindre des objectifs définis, ce qui permet aux ingénieurs de l'utiliser pour améliorer les performances et l'efficacité globales.
- Réduction du délai de commercialisation : L'optimisation topologique est un processus automatisé qui, avec une puissance de calcul suffisante, peut être effectué assez rapidement. Elle permet également d'éviter les itérations de conception manuelles par tâtonnements, qui nécessiteraient chacune des simulations distinctes.
- Optimisation de la méthode de fabrication : En incluant des contraintes de fabrication, les outils d'optimisation topologique résolvent le problème de génération d'une géométrie qui ne peut pas être fabriquée. Les ingénieurs sont en mesure de spécifier la méthode de fabrication prévue et d'optimiser les fonctionnalités en conséquence, réduisant ainsi les coûts et les délais.
- Exploration des matériaux alternatifs : Lorsque les ingénieurs choisissent d'utiliser un nouveau matériau, la conception peut nécessiter des modifications importantes de la géométrie de l'objet. Les outils d'optimisation topologique permettent aux ingénieurs de commencer par l'ancienne conception, puis d'insérer le nouveau matériau et de modifier la géométrie pour atteindre les objectifs de la conception.
Applications courantes de l'optimisation topologique
L'optimisation topologique est la plus couramment utilisée dans l'industrie aérospatiale, où les volumes de production sont faibles, les performances sont essentielles et les économies de poids offrent des avantages significatifs. Les premières applications aérospatiales se sont concentrées sur les supports qui maintiennent des objets lourds et subissent des charges importantes, tels que les supports de moteur.
Le succès remporté dans ce domaine a encouragé les entreprises aérospatiales à utiliser l'optimisation topologique pour d'autres composants structurels tels que les structures internes des ailes et les applications thermiques telles que les échangeurs de chaleur et les dissipateurs de chaleur. Bon nombre de ces pièces de production conçues à l'aide de l'optimisation topologique tirent parti de la fabrication additive, qui est bien comprise et bien adaptée aux applications aérospatiales.
L'industrie automobile est un autre secteur qui adopte l'optimisation topologique. La réduction du poids est un élément important de la conception des voitures et des motos, tout comme les économies associées à la baisse de la consommation de matériaux. L'impression 3D en grande quantité étant encore coûteuse, les constructeurs automobiles s'appuient fortement sur les contraintes de fabrication des outils d'optimisation topologique pour produire des géométries qui peuvent être fabriquées à l'aide de processus de fabrication en grande quantité tels que le pliage de tôle, l'emboutissage de métal et le moulage.
Les équipes de conception automobile tirent également parti de la possibilité d'inclure une analyse des vibrations dans l'étude d'optimisation topologiquee afin d'optimiser les performances en matière de bruit, vibrations et secousses (NVH) des véhicules, évitant ainsi les vibrations que les passagers peuvent entendre ou ressentir.
Les avantages de l'optimisation topologique s'appliquent également à de nombreux autres secteurs, notamment l'énergie éolienne et la construction de structures. Toute application qui permet à la charge de déterminer la forme du produit peut bénéficier de l'optimisation topologique. Les concepteurs explorent même son utilisation pour la conception de meubles, afin de créer des chaises et des tables fonctionnelles et naturelles.
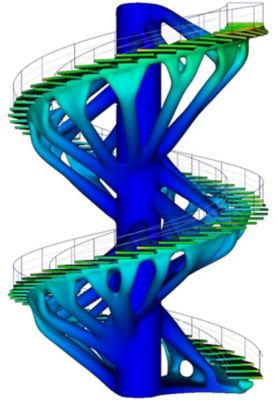
Cet escalier en colimaçon illustre la beauté naturelle des conceptions générées à l'aide de l'optimisation topologique.
Outils de simulation pour l'optimisation topologique
Les outils de simulation, généralement des progiciels d'analyse par éléments finis, constituent la technologie qui sous-tend l'optimisation topologique. Ils sont reliés à des outils d'optimisation topologique qui modifient les paramètres des éléments du modèle. Ces outils peuvent être classés en deux catégories : l'exploration de la conception préliminaire et la simulation détaillée.
Les outils de simulation de conception préliminaire rapides et faciles à utiliser, tels que le logiciel Discovery, concilient précision et rapidité pour offrir aux ingénieurs concepteurs des outils d'exploration rapide de la conception qui permettent d'étudier les formes optimales en temps quasi réel. Outre la vitesse, un lien étroit avec la géométrie CAD est important pour ce niveau d'optimisation topologique. Pour rendre l'optimisation topologique pratique, les outils de simulation modernes utilisent l'accélération GPU pour obtenir des solutions jusqu'à 10 fois plus rapides.
Une fois l'orientation de la conception établie, l'étape suivante consiste à déployer un outil de simulation détaillé tel que le logiciel Ansys Mechanical ou le logiciel Ansys LS-DYNA. Ces logiciels offrent des algorithmes avancés d'optimisation topologique, un large éventail de contraintes de conception et de fabrication, ainsi que des fonctionnalités de simulation multiphysique de classe mondiale. Une partie importante du processus d'optimisation consiste à exécuter une simulation de vérification précise et approfondie de la configuration finale afin de s'assurer que la conception optimisée répond à toutes les exigences de conception.
Ressources connexes
Commençons
Si vous êtes confronté à des défis d'ingénierie, notre équipe est là pour vous aider. Forts de notre expérience et de notre engagement en faveur de l'innovation, nous vous invitons à nous contacter. Collaborons pour transformer vos obstacles techniques en opportunités de croissance et de réussite. Contactez-nous dès aujourd'hui pour entamer la conversation.