-
-
Accédez au logiciel étudiant gratuit
Ansys donne les moyens à la prochaine génération d'ingénieurs
Les étudiants ont accès gratuitement à un logiciel de simulation de classe mondiale.
-
Connectez-vous avec Ansys maintenant !
Concevez votre avenir
Connectez-vous à Ansys pour découvrir comment la simulation peut alimenter votre prochaine percée.
Pays et régions
Espace client
Support
Communautés partenaires
Contacter le service commercial
Pour les États-Unis et le Canada
S'inscrire
Essais gratuits
Produits & Services
Apprendre
À propos d'Ansys
Back
Produits & Services
Back
Apprendre
Ansys donne les moyens à la prochaine génération d'ingénieurs
Les étudiants ont accès gratuitement à un logiciel de simulation de classe mondiale.
Back
À propos d'Ansys
Concevez votre avenir
Connectez-vous à Ansys pour découvrir comment la simulation peut alimenter votre prochaine percée.
Espace client
Support
Communautés partenaires
Contacter le service commercial
Pour les États-Unis et le Canada
S'inscrire
Essais gratuits
INFORMATIONS SUR LE SUJET
Qu'est-ce que la dynamique explicite ?
La dynamique explicite fait référence aux modèles numériques qui représentent un comportement dynamique non linéaire et dynamique, qui utilisent la méthode des éléments finis (FEM) avec une approche d'intégration temporelle explicite pour calculer la réponse aux charges appliquées sur de petits incréments de temps.
L'intégration temporelle explicite est la mieux adaptée aux problèmes non linéaires dont le comportement dépend du temps sur de courtes durées. Les applications typiques de l'analyse dynamique explicite comprennent les tests de chute, les collisions de véhicules, le formage des métaux et la rupture des matériaux.
La simulation de l'analyse par éléments finis (FEA) peut également utiliser une approche d'intégration temporelle implicite. L'approche explicite implique de nombreux petits pas de temps avec des calculs efficaces, alors que la méthode implicite utilise des pas plus grands mais moins nombreux. Les calculs sont également beaucoup plus coûteux. L'approche la plus adaptée est déterminée par la non-linéarité globale du système et la durée de l'événement.
Méthode des éléments finis
La méthode des éléments finis est une méthode mathématique utilisée pour résoudre des équations différentielles ordinaires ou partielles (EDP). Pour la simulation des systèmes physiques, les utilisateurs divisent le domaine en segments discrets, appelés éléments finis, et le logiciel applique des équations différentielles partielles à chaque élément. L'outil assemble ensuite les équations et les inconnues sont résolues à l'aide de solveurs numériques. L'utilisation de la méthode des éléments finis pour modéliser des systèmes physiques est appelée analyse par éléments finis (FEA).
Non linéaire
Dans l'analyse par éléments finis, le terme « non linéaire » fait référence à un comportement dans lequel l'équation représentative n'est pas linéaire. Le comportement non linéaire typique comprend des modèles de matériaux non linéaires, des grandes déformations, des conditions aux limites, des charges dynamiques, des contacts complexes et une défaillance des matériaux.
Simulation dynamique
L'équation complète du mouvement d'un objet est la suivante :
Force = (masse x accélération) + (amortissement x vitesse) + (rigidité x déplacement)
En cas d'accélération minimale ou de vitesse constante, un problème peut être qualifié de statique. Dans ce scénario, un solveur FEA doit uniquement déterminer les valeurs inconnues de la force et du déplacement ; le facteur temps n'entre pas en jeu. Cependant, si la vitesse change, le problème est dit dynamique car des changements se produisent au fil du temps.
Méthode d'intégration temporelle explicite
Les équations différentielles partielles d'un modèle par éléments finis représentant des événements dynamiques sont résolues à un pas de temps donné. Par conséquent, le logiciel doit intégrer les équations différentielles partielles au fil du temps. L'approche dynamique explicite est dite « explicite » car le résultat de l'intégration est une équation qui calcule explicitement la valeur au pas de temps suivant pour les quantités connues au pas de temps actuel. L'autre méthode utilisée dans l'analyse par éléments finis, l'intégration de temps implicite, est dite « implicite » car la valeur souhaitée au pas de temps suivant n'est déterminée qu'indirectement, par le biais d'une équation impliquant à la fois des quantités connues et inconnues. Dans ce cas, le solveur utilise l'algèbre linéaire pour calculer les inconnues implicites.
Un exemple de méthode explicite, la méthode d'Euler progressive, aboutit à une équation qui n'est qu'une fonction du pas de temps actuel :
$$y_{k+1} = y_k - \Delta t \, y_k^2 $$
Principaux aspects de l'analyse dynamique explicite
Lors de l'utilisation de la méthode de solution dynamique explicite dans un logiciel de simulation, les débutants en simulation et les ingénieurs expérimentés doivent être conscients de certains aspects importants de la méthodologie, qui sont déterminés par les algorithmes mathématiques utilisés par l'approche.
Pas de temps critique et temps de propagation des ondes
L'information la plus importante à considérer est que la solution explicite résout le pas de temps juste après le pas de temps actuel. Dans la mesure où le solveur calcule la manière dont la déformation évolue au cours du pas de temps, la taille du pas de temps est limitée au temps nécessaire à une onde de déformation pour traverser le plus petit élément du modèle. Cette limite est appelée le pas de temps critique, et la vitesse à laquelle le son traverse le matériau détermine le temps de propagation des ondes. Pour les matériaux rigides et les éléments de petite taille, le pas de temps critique est généralement de l'ordre de la milliseconde.
Comportement non linéaire
L'aspect suivant dont les ingénieurs doivent être conscients concerne les différents types de comportements non linéaires que la dynamique explicite peut capturer. Dans la mesure où l'approche explicite utilise des pas de temps aussi petits, elle peut traiter la modification d'une valeur calculée au cours de ce petit pas de temps comme un comportement linéaire.
Les ingénieurs classent la plupart des comportements non linéaires issus d'une simulation FEA dans l'une des catégories suivantes :
1. Matériaux non linéaires
Les matériaux non linéaires ont des propriétés qui changent de manière non linéaire sous l'effet de la charge ou du temps. Dans quasiment tous les types d'analyses, la forme la plus courante de non-linéarité des matériaux est la plasticité. L'approche implicite peut avoir des difficultés à déterminer la convergence pour des niveaux de plasticité plus élevés, en particulier lorsque la rigidité du matériau diminue. Les propriétés dépendant de la vitesse de déformation, telles que la rigidité, sont étroitement liées à la plasticité. Une autre forme de non-linéarité des matériaux implique des changements brusques des propriétés des matériaux, en particulier de la rigidité, souvent causés par des changements de phase ou par la rupture du matériau.
2. Géométrie non linéaire
La forme la plus courante de comportement géométrique non linéaire est la grande déformation. C'est là que la formulation à faible vitesse de déformation utilisée dans l'analyse statique linéaire n'est plus valable. Une autre forme de géométrie non linéaire est le mouvement de corps rigide, dans lequel le centre de masse du corps se déplace au fil du temps ou l'objet est en rotation autour d'un point.
3. Conditions aux limites et charges non linéaires
Dans une analyse implicite, la convergence devient difficile à obtenir lorsqu'une charge change rapidement par rapport au pas de temps. Il peut s'agir d'une charge appliquée ou d'une charge transmise par contact entre deux corps.
Les événements à grande vitesse et de courte durée présentent souvent ces types de non-linéarités. Les petits pas de temps utilisés dans l'intégration temporelle explicite permettent d'estimer ces changements comme étant linéaires d'un pas à l'autre. Ils permettent également au solveur de calculer les forces internes qui maintiennent l'équilibre des systèmes non linéaires pendant la rupture de la plasticité ou du matériau.
Approximation de la masse concentrée
L'approche d'intégration temporelle explicite utilisée pour résoudre les problèmes dynamiques présente un autre aspect essentiel : la possibilité de représenter la masse nodale de chaque élément comme une masse concentrée. Cela produit une matrice de masse avec une seule diagonale, de sorte que l'inversion de matrice nécessaire pour calculer les valeurs d'inertie du modèle est insignifiante.
Analyse structurelle quasi-statique
Un sous-ensemble d'analyses structurelles dynamiques se produit lorsque les effets d'inertie dans un système sont suffisamment faibles pour être ignorés et que le système reste essentiellement en équilibre toute la durée. Le formage des métaux est un bon exemple de ce type de comportement. Il est dynamique dans la mesure où les propriétés du matériau, en particulier la plasticité, dépendent du temps, mais l'inertie du métal n'a pas d'incidence sur sa déformation plastique.
Qu'est-ce que la dynamique implicite ?
Il est difficile de parler de dynamique explicite sans parler de dynamique implicite. Comme son nom l'indique, la dynamique implicite est une approche de simulation FEA qui utilise un schéma d'intégration temporelle implicite. Tout comme la dynamique explicite, la dynamique implicite résout toujours l'équation complète du mouvement au fil du temps avec plusieurs pas de temps.
Les équations de la méthode d'intégration implicite impliquent des valeurs pour le pas de temps actuel et pour le pas de temps suivant. Pour les outils logiciels de simulation implicite, le solveur utilise une méthode d'Euler implicite pour dériver des équations d'une certaine valeur au pas de temps suivant qui sont une fonction du pas de temps actuel (k) et du pas de temps suivant :
$$y_{k+1} = \frac{-1 + \sqrt{1 + 4 \Delta t y_k}}{2 \Delta t} $$
La différence entre la méthode implicite et les méthodes explicites
Les ingénieurs utilisent les deux approches d'intégration dans l'analyse structurelle, pour les simulations dynamiques et quasi-statiques. Comme mentionné dans l'introduction, la principale différence réside dans le fait que, lorsque les équations différentielles partielles sont intégrées dans la méthode explicite, la solution est entièrement définie par l'équation résultante. Dans la méthode implicite, les valeurs inconnues sont implicites. L'algorithme doit donc utiliser l'algèbre linéaire pour trouver la solution.
D'un point de vue concret et pratique, cela se traduit par les différences suivantes :
| Méthode implicite | Méthode explicite | |
| Taille du pas de temps | Définie par l'utilisateur pour capturer les changements de charge et faciliter la convergence des calculs non linéaires. Le pas de temps est grand, nécessitant peu d'étapes. | Définie par le temps de propagation des ondes à travers le plus petit élément du maillage. La taille du pas de temps est exprimée en millisecondes ; de nombreux pas sont ainsi nécessaires, même pour de courtes durées. |
| Calcul des cycles par pas | Solution complète d'équations simultanées. Plusieurs résolutions par pas de temps si les calculs non linéaires doivent converger. | Solution explicite très efficace pour chaque pas avec une masse concentrée facilement inversée. |
| Exigences en matière de mémoire | La méthode d'intégration implicite et la matrice de masse complète nécessitent beaucoup plus de mémoire que les méthodes explicites. | La méthode d'intégration explicite et la formulation de masse concentrée nécessitent beaucoup moins de mémoire que les méthodes implicites. |
| Convergence | La convergence doit être assurée à chaque pas de temps pour les calculs non linéaires, en établissant l'équilibre. | Elle n'est pas nécessaire car un petit pas de temps permet une hypothèse linéaire. |
| Équilibre | Requis | Non requis |
| Sensibilité au nombre de mailles pour les ressources de calcul | Dépend du problème, car la bande passante de la matrice résultante détermine les temps de résolution. | Dépend linéairement du nombre d'éléments. |
| Sensibilité à la taille des éléments | La durée d'exécution est relativement indépendante de la taille des éléments individuels. | Dépend linéairement de la plus petite taille d'élément. La réduction de moitié du plus petit élément double la durée d'exécution. |
| Contact | Itération requise jusqu'à ce que l'équilibre des forces soit atteint. La solution peut diverger en cas de changements de contact brusques. | Aucune itération n'est nécessaire. Bonne prise en charge des changements brusques de contact . |
| Rupture du matériau | La suppression de la rigidité d'un élément ou de la connexion entre éléments peut entraîner des problèmes de convergence et nécessite souvent un maillage adaptatif. | Bonne prise en charge grâce aux petits pas de temps. |
| Non-linéarités du matériau | Des changements brusques de propriétés et une faible rigidité peuvent entraîner des problèmes d'équilibre et, par conséquent, des problèmes de convergence. | Un petit pas de temps permet un traitement linéaire au cours d'un pas de temps donné. |
Exemples de simulation dynamique explicite
La petite taille du pas de temps et la formulation de masse concentrée utilisées dans l'analyse dynamique explicite la rendent idéale pour les événements de courte durée présentant des non-linéarités significatives. Les utilisateurs peuvent choisir cette approche plutôt que l'analyse implicite pour les événements plus longs, quasi-statiques présentant des problèmes d'équilibre.
Les ingénieurs peuvent utiliser les solutions dynamiques explicites d'Ansys telles que le logiciel Ansys LS-DYNA, dans différents secteurs afin de générer rapidement des informations utiles pour des simulations structurelles non linéaires extrêmement complexes. Vous trouverez ci-dessous une liste de certaines des applications les plus courantes.
Test de chute
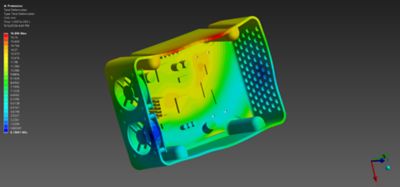
Les produits grand public et industriels doivent résister à des chutes d'une hauteur raisonnable lors du transport et de l'utilisation. C'est pourquoi les ingénieurs utilisent donc les normes industrielle pour les tests de chute, afin de s'assurer que leurs produits sont suffisamment robustes. Toutefois, les tests physiques sont coûteux et nécessitent un matériel réel. L'utilisation d'un outil tel que le logiciel LS-DYNA, qui peut se connecter aux modèles de conception assistée par ordinateur (CAO) via la plateforme Ansys Workbench, réduit les coûts et fait intervenir les tests de chute virtuelles à un stade plus précoce et moins coûteux du processus de développement du produit.
Collisions impliquant des véhicules

Parmi toutes les applications de simulation dynamique explicite, l'analyse et la simulation des accidents de voiture sont probablement celles qui ont touché le plus de personnes et sauvé d’innombrables vies. La collision d'un véhicule avec un obstacle solide ou un autre véhicule implique l'écrasement et la rupture de structures métalliques sur une courte période de temps ; une application idéale pour la dynamique explicite. C'est pourquoi tous les constructeurs automobiles simulent des véhicules complets, des systèmes de ceintures de sécurité, des airbags et des batteries à l'aide d'une application telle que le logiciel LS-DYNA ou d'outils logiciels similaires.
Collisions impliquant le corps humain

Les événements de courte durée qui exercent une force sur un objet se produisent non seulement avec les produits et les machines, mais affectent également le corps humain. C'est pourquoi les ingénieurs intègrent dans leurs simulations dynamiques explicites des modèles structurels de haute fidélité du corps humain, tels que le modèle Ansys Hans. Plus qu'un simple mannequin constituant une forme et une masse, ce modèle structurel humain détaillé permet de représenter les charges et les zones de blessure associées à n'importe quelle partie de l'anatomie humaine dans diverses situations, qu'il s'agisse de collisions de voitures de course ou d'un coup porté à la tête.
Simulation cardiaque
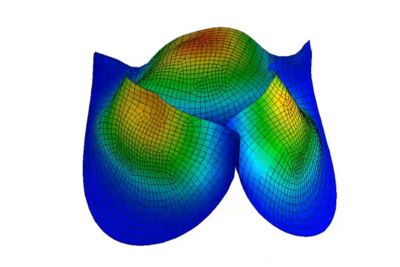
Le cœur humain est l'un des exemples les plus complexes de la multiphysique structurelle. Les impulsions électriques déclenchent d'importantes déformations dans les tissus musculaires, qui à leur tour pompent le sang à travers des valves qui s'ouvrent et se ferment. Les chercheurs et les ingénieurs modélisent cette interaction dynamique, y compris la dynamique des fluides numérique (CFD) comme le flux sanguin, dans un véritable outil de dynamique explicite multiphysique tel que le logiciel LS-DYNA.
Formage des métaux
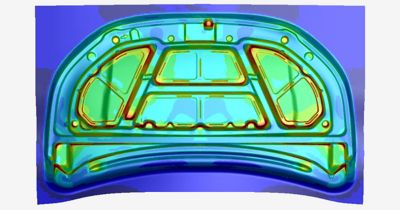
L'homme façonne le métal depuis l'âge du bronze. Mais à l'ère du silicium, nous mettons à profit la simulation dynamique explicite pour optimiser le processus. L'étape du formage, au cours de laquelle un outil rigide plie et façonne de fines tôles, est une application idéale de la méthode dynamique explicite dans l'analyse par éléments finis. En revanche, les processus tels que le retour élastique et le traitement thermique durent plus longtemps et sont mieux résolus par une analyse implicite. Grâce à cela, les ingénieurs peuvent utiliser une chaîne de simulation qui déplace la simulation d'un outil explicite tel que le logiciel LS-DYNA vers le solveur implicite du même outil ou vers une application logicielle distincte telle que le logiciel d'analyse structurelle par éléments finis Ansys Mechanical.
Soudure par refusion
Les fabricants de semi-conducteurs produisent chaque année des millions de micropuces qui sont reliées physiquement et électriquement par de minuscules billes de soudure. La qualité de ces billes de soudure a un impact sur les performances, le refroidissement et la robustesse de quasiment tous les produits électroniques. La simulation dynamique explicite est capable de gérer le comportement hautement non linéaire du métal d'apport lorsqu'il fond, s'écoule sous l'effet de la tension superficielle puis se solidifie.
Il ne s'agit là que de quelques-unes des applications les plus courantes des outils logiciels de dynamique explicite. Parmi les autres utilisations, citons :
- Les applications de défense, en particulier celles qui concernent les munitions et les armures. Le logiciel Ansys Autodyn est un outil particulièrement adapté à ce type de problèmes.
- Processus d'usinage tels que le fraisage et le tournage pour optimiser la conception de l'outil et la vitesse d'usinage
- Comportement de ballottement dans les conteneurs lors des manœuvres des véhicules
- Flambage des structures sous des charges critiques
- Articles de sport soumis à des événements dynamiques de courte durée
Les progrès en matière de capacités des solveurs, d'interfaces utilisateur et de puissance de calcul ont considérablement élargi l'utilisation de la dynamique explicite. Autrefois limitée aux applications de pointe de l'aérospatiale et de la défense (A&D), cette méthode est désormais utilisée dans la conception automobile et dans de nombreux autres domaines. Elle est particulièrement utile dans les situations impliquant des charges ou des non-linéarités brèves mais intenses que les solveurs d'intégration temporelle implicites traditionnels peinent à traiter.
Des fournisseurs de premier plan comme Ansys proposent également une formation et une assistance complètes, ainsi que des exemples pour aider les ingénieurs à maîtriser leurs conceptions et à améliorer leurs performances, leur sécurité et leur durabilité.
Ressources connexes
Commençons
Si vous êtes confronté à des défis d'ingénierie, notre équipe est là pour vous aider. Forts de notre expérience et de notre engagement en faveur de l'innovation, nous vous invitons à nous contacter. Collaborons pour transformer vos obstacles techniques en opportunités de croissance et de réussite. Contactez-nous dès aujourd'hui pour entamer la conversation.